モデル化とは、何らかの物事について、より簡単に考えられるように細部を簡略化し、注目する特徴だけを図や数式など他の分かりやすい形式で表現することです。現実のものを抽象的な表現に変換することで、コンピューターでも扱いやすくなります。当記事では、モデル化の具体例や、情報科学におけるモデル化の基本的な用語についてまとめます。
このページでは、
- モデル化
- ネットワークモデル・グラフ
- 階層モデル・木構造
を解説しています。
モデル化とは
導入部分でも述べましたが、モデル化とは、何らかの物事について、より簡単に考えられるように細部を簡略化し、注目する特徴だけを他の分かりやすい形式で表現することです。モデル化することのメリットは、物事を単純化することでシンプルかつ効率的に考えることができるようになることです。
表し方としては、図、数式、表、立体模型など様々ありますが、物事の特徴を抜き出し抽象的な表現に変換することが核となります。いくつか例を見てみましょう。
例1:路線図
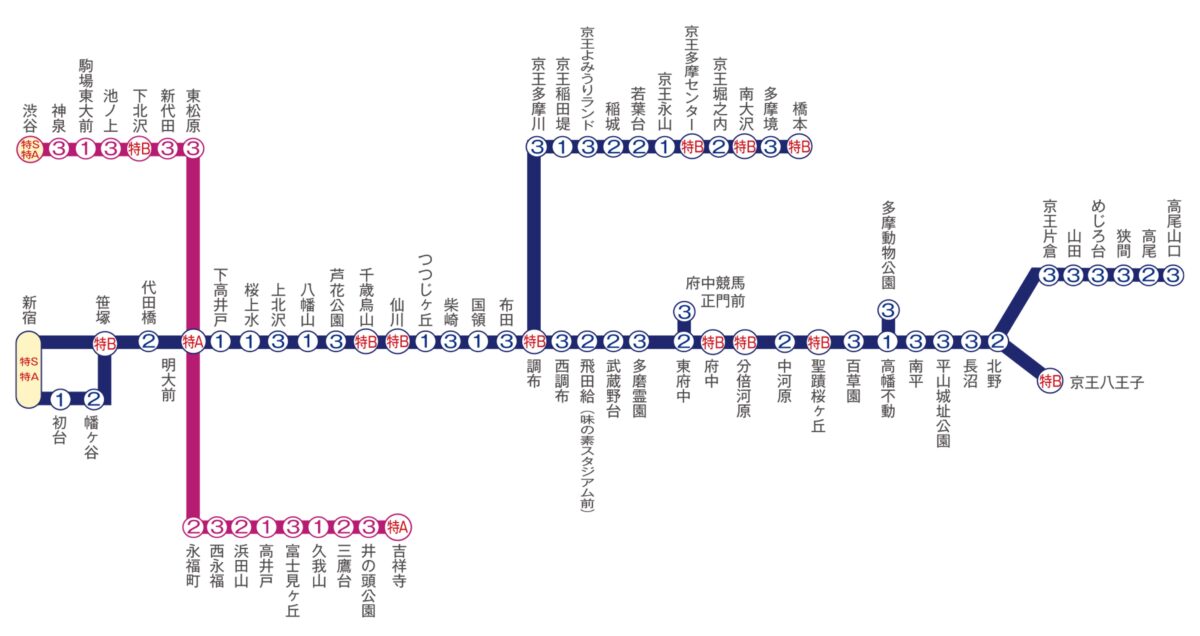
縮尺や方角などのディテールをそぎ落とし、駅どうしのつながりだけを表現しています。
例2:現実世界の動きを数式化する
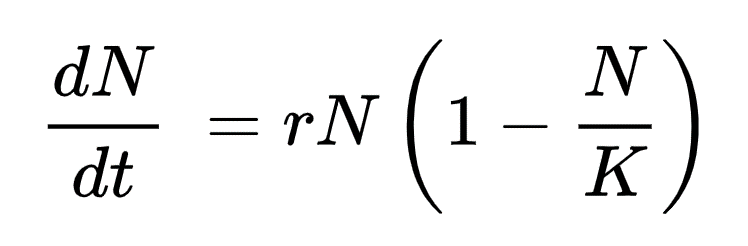
上式のロジスティクス方程式は、生物の個体数の変化を数式で表した、基本的な数理モデルの1つです。個体数が多いほど増殖も速くなる、食料などの問題から増殖には限界がある、などの現実世界の性質を単純化し数式で表現しています。
※ここでは数式を理解する必要はありません。
用語まとめ
いくつかの代表的なモデルとそれに関連する用語を紹介します。
ネットワークモデル
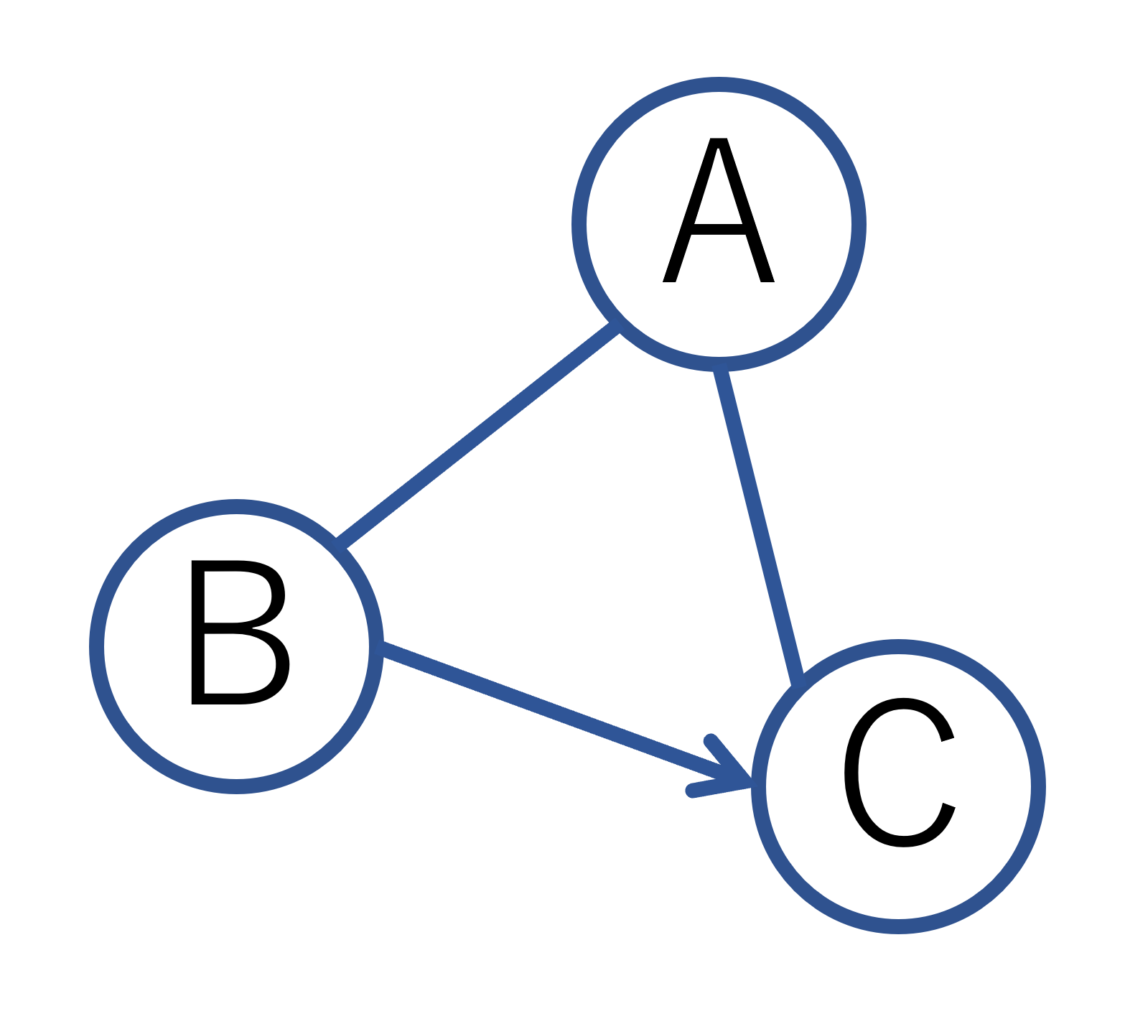
路線図のようにつながりを表現するモデル一般をネットワークモデルといいます。そしてこのネットワークモデルを表現する手法の1つが、上図のようなグラフです。
ここでいう「グラフ」とは、折れ線グラフや棒グラフの類ではなく、数学のグラフ理論で登場する表現方法のことです。大学入試史上最難と名高い1998年東大後期数学大問3で扱われたことでお馴染みかもしれません。
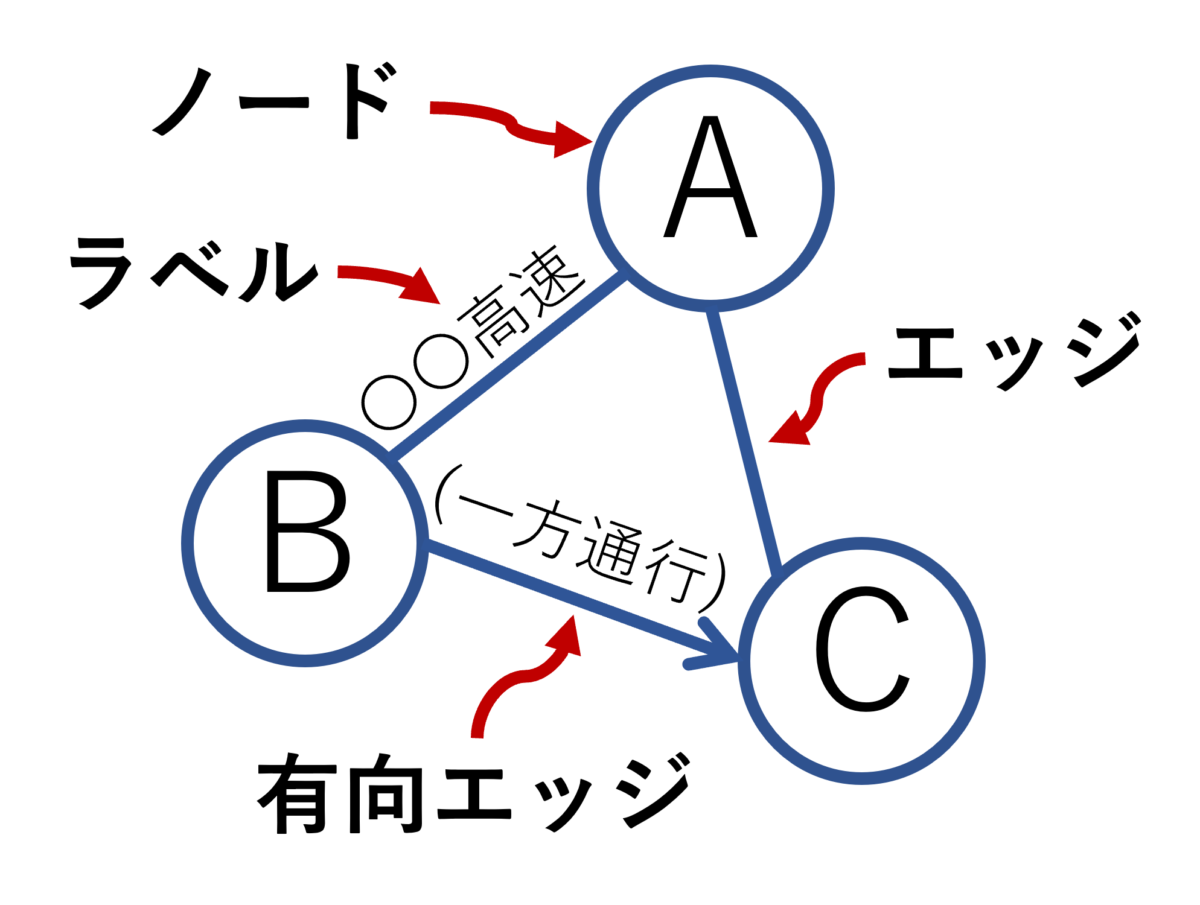
グラフにおいては、つながりを持つ物事を表す部分をノード、つながりを表す線をエッジ、向きを持つエッジを有向エッジ、エッジの名称を表す言葉をラベルといいます。
また、全てのエッジを重複せずたどる経路をオイラー路といいます。
グラフやオイラー路の考え方は、運輸や道路保守などはもちろん、工夫次第で様々に活用できます。「有限状態機械」では、グラフを基に様々な「計算」を行います。詳しくは下記のページを参照してください。
参考:一筆書きの条件
ちなみにグラフ理論において、オイラー路が存在する、すなわちグラフ(のエッジ)が一筆書きできる条件は、以下のいずれかを満たすことだと知られています。
- 全てのノードについて、偶数個のエッジがつながっている
- 全てのノードの中で、奇数個のエッジがつながっているものがちょうど2つある
※全てのエッジが他のエッジを介してつながっていることを前提とする。
1の場合を、一筆書きして戻ってこれる「オイラーグラフ」といい、2の場合を、スタートとゴールが異なる一筆書きができる「準オイラーグラフ」といいます。
階層モデル
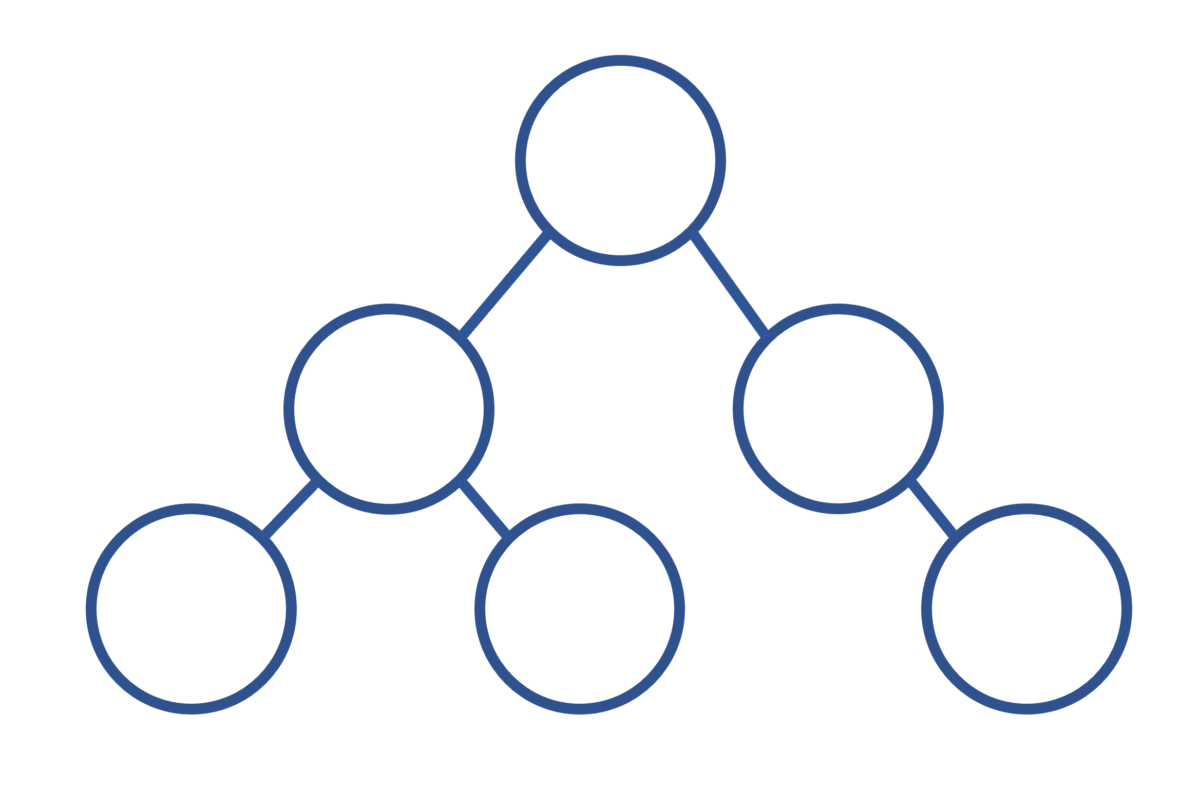

物事を分類するときに階層的な構造を作ることはよくあると思いますが、上図のような枝分かれを持つ「木構造」で表したモデルを階層モデルといいます。
例:ヒューマンエラーの分類を木構造で表した階層モデル
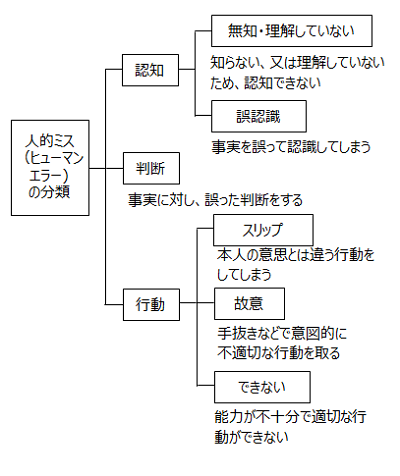

ヒューマンエラーをプロセスごとに分類することで適切な対策につなげる助けとしている。
住所や組織図なども木構造で表された階層モデルにあたります。
3行まとめ
このページではモデル化について解説しました。まとめると以下の通りです。
- 物事を注目する特徴のみに簡略化・抽象化し分かりやすい形式で表現することをモデル化という。
- グラフはネットワークモデルの表現方法の1つで、全エッジを重複せずたどる経路をオイラー路という。
- 階層モデルは木構造によって表される。
皆様の参考になれば幸いです。
当サイトでは教養としての情報科学を体系的に紹介しています。以下から当サイトの記事一覧をご覧いただけます。


