有限状態機械(有限オートマトン)とは、いくつかの「状態」とそれらの間の遷移規則を用いて問題を解く仕組みのことです。問題を解くという意味での「計算機」の中で、最も基本的な構造のひとつといえ、計算機科学の中でも重要な概念です。なにか具体的な機械があるわけではなく、抽象的な構造のことを指します。ここでいう「問題」や「計算」は、普段使っている言葉とは意味が少し違いますが、それを含めて具体例を交えて解説していきます。
このページでは、
- 有限状態機械とは
- 状態図・始状態・受理状態について
- チューリング機械について少し
を解説しています。
「問題」と「計算」
一般的に「問題」や「計算」といえば、足し算や掛け算などの数式を解いて答えを出すといったことを指すことが多いですが、ここでは、「様々な文字列について、ある条件を満たしているかどうか」を「問題」、それを判定することを「計算」と呼ぶことにします。例えば、「『○』と『×』からなる文字列について、『○』が3つ以上あるか」といった具合です。
では、この問題について有限状態機械を用いて考えてみましょう。
有限状態機械の考え方

有限状態機械(有限オートマトン)は、入力される文字列(長さは有限)を端から1文字ずつ読み取り、その度に処理を行うことにより入力された文字列が条件を満たすかどうか判断します。
下図のように、ヘッドが左から1文字ずつ読み取っていくようなイメージです。
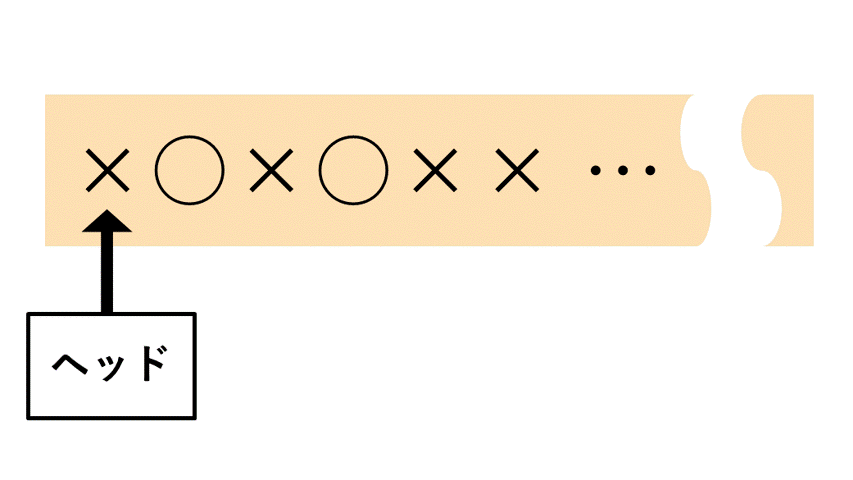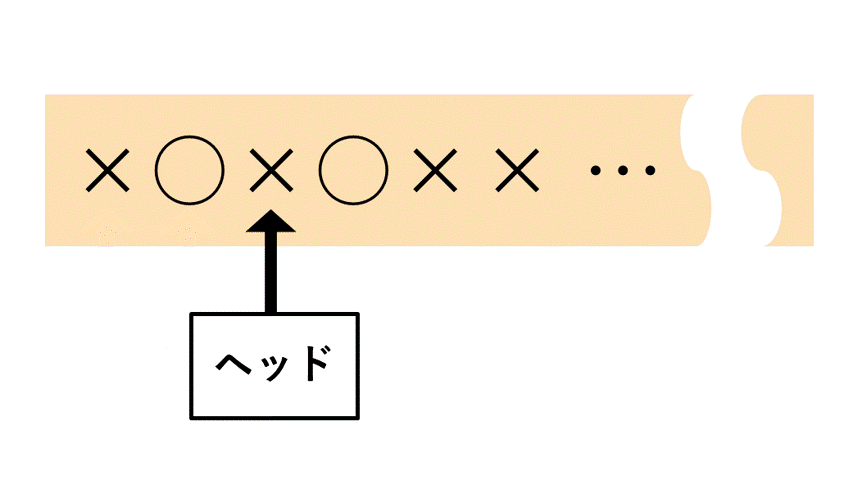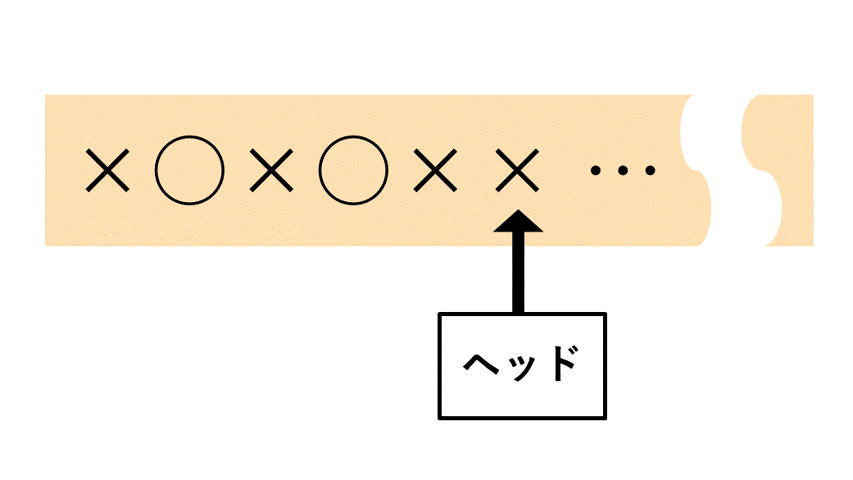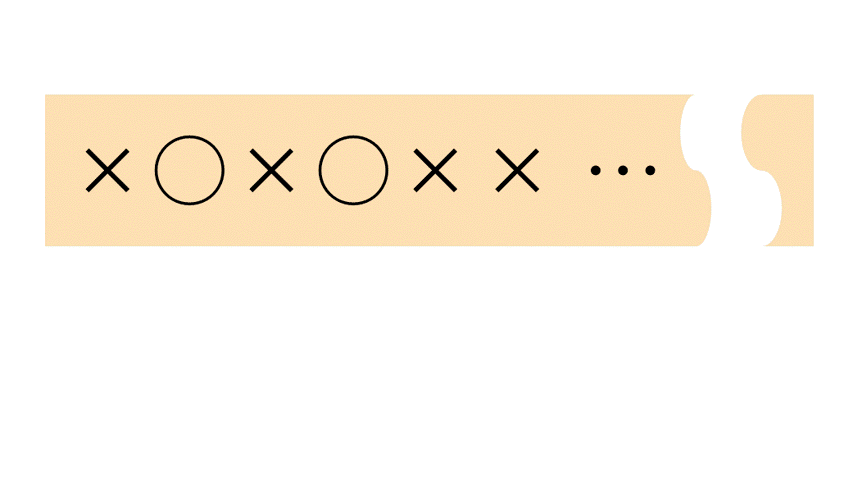
この問題に対する有限状態機械Aの構成は、以下のようなものが考えられます。
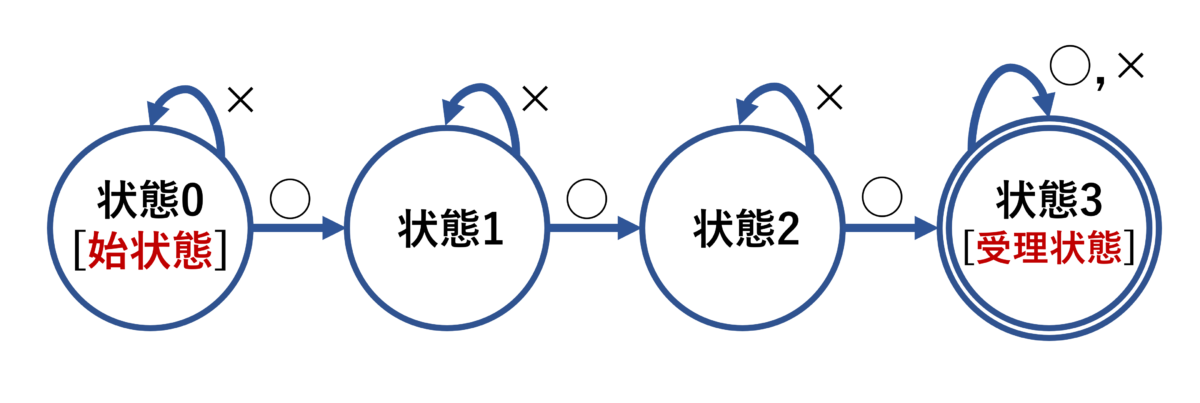
このような有限状態機械の構造を表す図を「状態図」といいます。
始め、Aは「状態0」にあります。これを「始状態」といいます。次に以下のような処理が行われます。
1文字目を読み取る→「×」→「状態0」にとどまる
2文字目を読み取る→「○」→「状態1」に進む
3文字目を読み取る→「×」→「状態1」にとどまる
4文字目を読み取る→「○」→「状態2」に進む
5文字目を読み取る→「×」→「状態2」にとどまる
・・・
上記のように、状態図に示されている状態間の「遷移規則」に従い、文字列の最後に達するまでこのように処理を繰り返していきます。また、名前の通り状態は有限個です。
今回の場合、最終的に「状態3」に達していれば、文字列に「○」が3つ以上含まれていたと分かります。今回の「状態3」のように、条件を満たしているときにある状態のことを「受理状態」といいます。また、条件を満たしていると判断することを「受理する」、満たさないと判断することを「拒否する」といいます。
問題の構造を抽象的にとらえ、今回の場合、「状態1」を「○が1つ確認された状態」、「状態2」を「○が2つ確認された状態」、「状態3」を「○が3つ以上確認された状態」と設定しているのです。
なお、有限状態機械を設計する際は、想定されるあらゆる入力値について対応できるものにしなければならない点に注意しなくてはなりません。
練習問題
有限状態機械の基本がわかったところで、有限状態機械の構造を自分で考えてみましょう。
問題
以下のような1桁以上の2進数の数値について、数を左端から読み取り数値が3の倍数かどうかを判定する有限状態機械の構造を示す状態図を描け。
101001…0110
↓解答↓
↓
↓
解答
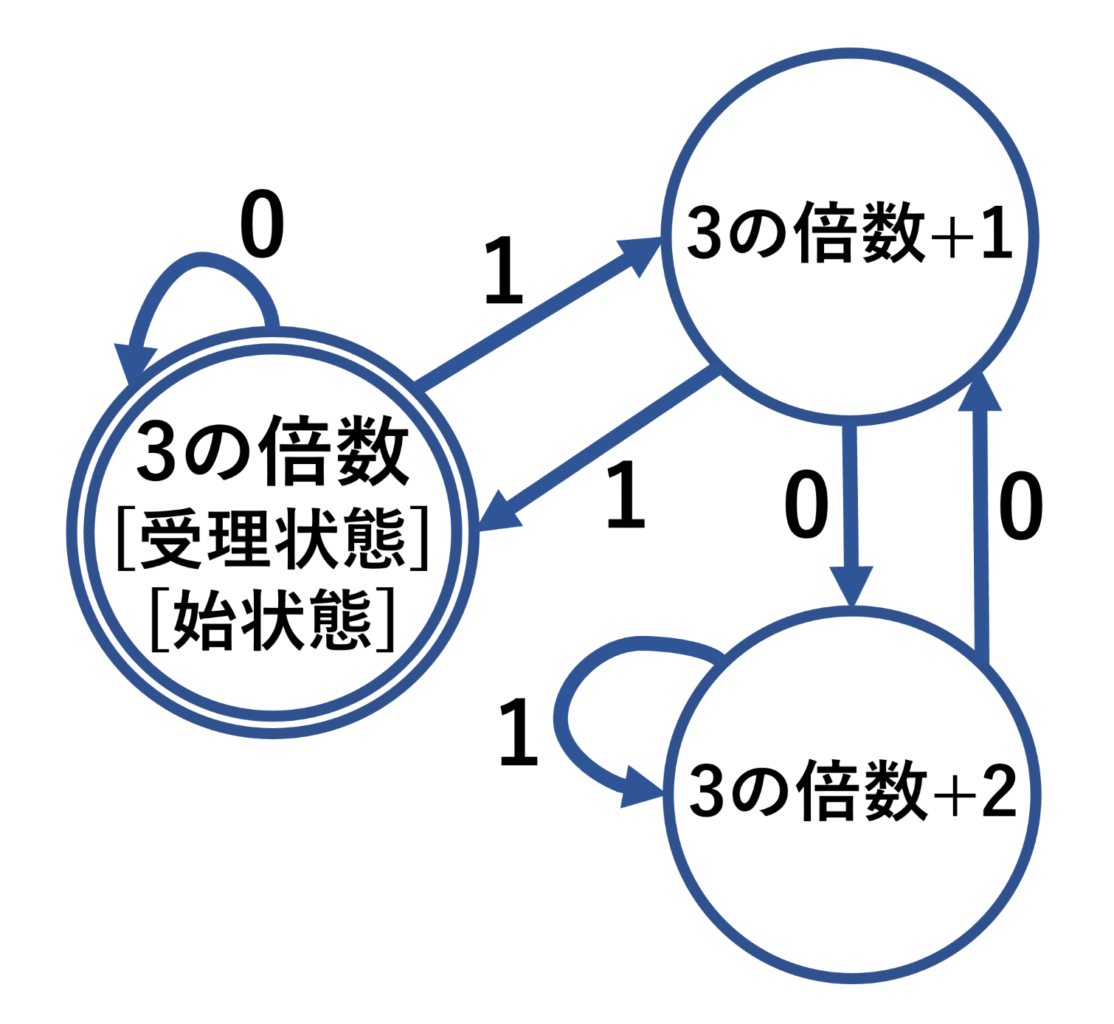
まず全ての数値は「3の倍数」、「3の倍数+1」、「3の倍数+2」のいずれかに分類されます。そこで、「3の倍数」を始状態と受理状態に設定します。2進数の数値の末尾に0が追加されると、数値は2倍になり、末尾に1が追加されると数値は2倍に1を足したものになります。このことから、以下のように考えることができます。
「3の倍数」 +「末尾0」→「3の倍数」
「3の倍数」 +「末尾1」→「3の倍数+1」
「3の倍数+1」+「末尾0」→「3の倍数+2」
「3の倍数+1」+「末尾1」→「3の倍数」
「3の倍数+2」+「末尾0」→「3の倍数+1」
「3の倍数+2」+「末尾1」→「3の倍数+2」
これを状態図に表すと上記のようになります。
状態図は数学の確率漸化式の分野でなじみがある方もいるでしょう。考え方は同じです。様々な状態をいくつかに分類し、その間の遷移規則を考えていくということです。
【発展】チューリング機械
有限状態機械の発展形として、チューリング機械(チューリングマシン)があります。これは、有限状態機械と比べて次のような違いを持ちます。
- ヘッドが一方向ではなく左右に1文字ずつ動く
- ヘッドが文字列を読むだけでなく変更できる
- 文字列は左右に無限に並べることができる
現在の実際の計算機は、全てこのチューリング機械の原理に基づいて動いていると考えることができます。つまり、どのようなアルゴリズムであっても、それを実行するチューリング機械の構造を考えることができるということです。裏を返せば、ある問題についてそれを解くチューリング機械の構造が考えられないのであれば、その問題はコンピューターで解くことはできません。
チューリング機械は、1936年にイギリスの数学者・計算機科学者であるアラン・チューリングが提唱しました。チューリングはコンピューターや計算の原理的な理論において大きな功績を残しています。
また、第二次世界大戦中にはドイツ軍の暗号機「エニグマ」による暗号を解読する機械を開発しました。映画「イミテーション・ゲーム/エニグマと天才数学者の秘密」では、このエニグマの解読を中心に、彼の激動の人生が描かれています。映画としても評価が高い一作です。ぜひご覧になってはいかがでしょうか。

(1912-1954)
(Wikipediaより)
3行まとめ
このページでは有限状態機械について解説しました。まとめると以下の通りです。
- 有限状態機械は、文字列を1文字ずつ読み取り状態を遷移させていくことで条件が満たされているか判断する。
- その構造は状態図で表され、始状態から始まり受理状態に達すれば条件が満たされていると判断できる。
- 状態図を描くには、まず考えられる状態を分類し、その間の遷移規則を考える。
皆様の参考になれば幸いです。
当サイトでは教養としての情報科学を体系的に紹介しています。以下から当サイトの記事一覧をご覧いただけます。

