「情報量」という言葉は日常的によく使われますが、情報理論では「何らかの情報について、それにどのぐらいの情報が含まれているかを数値で評価する指標」であり、数式で表現されます。ここでいう「情報」とは、「ある物事が起こるということを伝えるもの」であり、例えば「明日雨が降る」といったものです。やや難解なところもありますが、例を用いて丁寧に解説します。
このページでは、
- 情報量の定義と求め方
- 情報量の性質
- 平均情報量の定義と求め方
を解説しています。
情報量の定義
まず情報量の定義を確認します。
情報量の定義
ある物事Xが起こる確率を \(P(X)\)とすると、「Xが起こる」という情報の情報量 \(i(X)\)は、
$$i(X)=-\log_2 P(X)$$
と定義される。単位はビットである。
ここで、\(P(X)\)とは「現在持っている情報の下で物事Xが起こる確率」である。
これだけでは理解しにくいでしょうから、以下で例を使って解説します。
情報量の求め方の例
例を用いて情報量を考えてみましょう。
あなたは犯罪組織を追う捜査官だとします。組織の次の犯行は2月中に行われることが分かりました。しかしどの日に決行されるかはまだ分かりません。

例1
内通者から次の情報を得ました。
A:犯行は2月の前半に決行される

情報Aを得る前では、Aが起こる確率は \(P(A)=\frac{14}{28}=\frac{1}{2}\)です。よって、情報Aの情報量は、
$$i(A)=-\log_2 P(A)=-\log_2 \frac{1}{2}(=1)$$
となります。
例2
また、別の例として、次の情報を得たとします。
B:犯行は2月の第1週に決行される

情報Bを得る前では、Bが起こる確率は \(P(B)=\frac{7}{28}=\frac{1}{4}\)です。よって、情報Bの情報量は、
$$i(B)=-\log_2 P(B)=-\log_2 \frac{1}{4}(=2)$$
となります。
例3
最後に、情報Aを得ている状態で、情報Bを得たとします。

情報Aから2月の前半ということは既に分かっているので、情報Bを得る前では、Bが起こる確率は \(P(B)’=\frac{7}{14}=\frac{1}{2}\)です。よって、この場合の情報Bの情報量は、
$$i(B)’=-\log_2 P(B)’=-\log_2 \frac{1}{2}(=1)$$
となります。
このように、情報量は受け取り手の状況によって変化します。
情報量の性質
情報量の求め方は分かりましたでしょうか。では、次に情報量の性質を確認して、なぜ情報量は \(-\log_2 P(X)\)と定義されるのか考えてみましょう。
性質1:珍しいことは情報量が多い
先ほどの例で、AとBはどちらが珍しいことでしょうか。

Aが起こる確率は\(\frac{1}{2}\)
Bが起こる確率は\(\frac{1}{4}\)
ですので、Bの方が珍しいことです。すなわち、情報としては「Bが起こる」の方が価値があり、情報量は大きくなるべきです。定義を見ると、確かに発生する確率が低いことが起きるとわかった時ほど、情報量は大きくなっています。
性質2:情報は足されていく
ここで、情報Bを持っている状態で、次の情報を得たとします。
C:犯行は水曜日に決行される
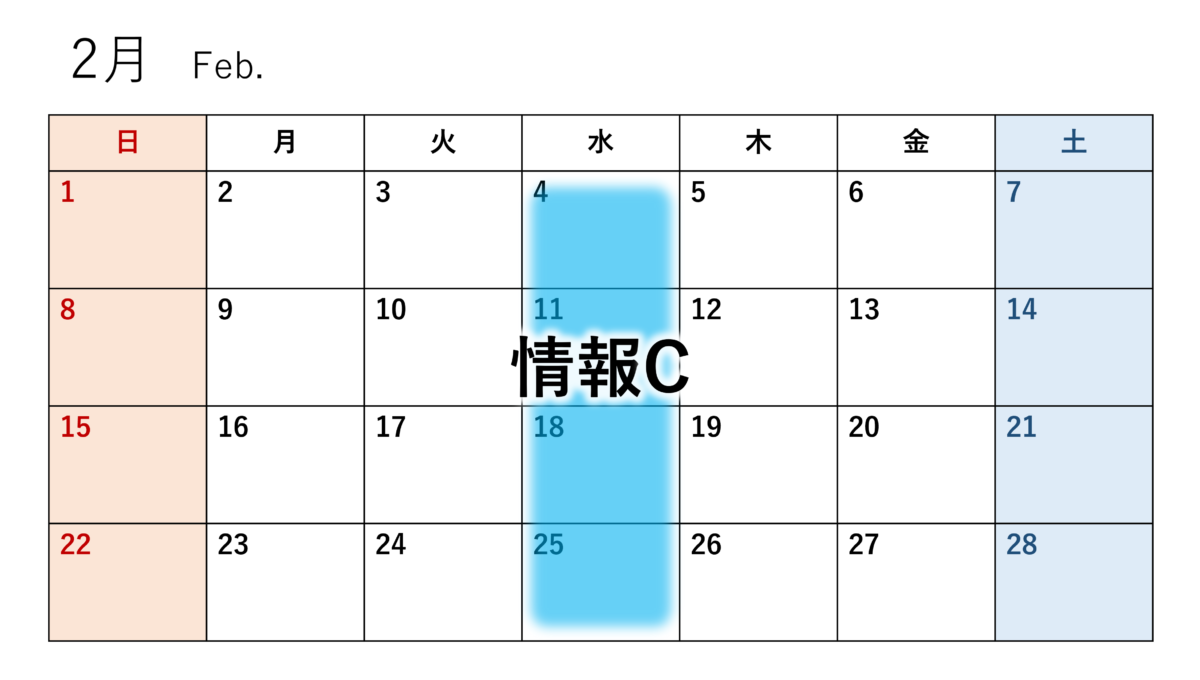
情報Cを得る前では、Cが起こる確率は \(P(C)=\frac{1}{7}\)です。よって、情報Cの情報量は、
$$i(C)=-\log_2 P(C)=-\log_2 \frac{1}{7}(=\log_2 7)$$
です。
B・Cが同時に起こる確率は \(P(B\cap C)=P(B)\cdot P(C)\)ですので、B・Cが同時に起こるという情報の情報量は、
$$i(B\cap C)=-\log_2 P(B\cap C)=-\log_2 P(B)\cdot P(C)=-\log_2 P(B)-\log_2 P(C)=i(B)+i(C)=2+\log_2 7$$
となります。このことから、以下のように、情報量は足し算で増えていくことが分かります。
$$i(B\cap C)=i(B)+i(C)$$
情報が増えると確率は掛け算されていきますが、対数で表されているので足し算に変換できます。情報量の加算を足し算で計算できるのが、対数が使われている大きな理由です。
性質3:情報量は情報を得る経路によらない
以下の情報を考えます。
D:犯行は2月4日(水)に行われる

Dが起こる確率は \(P(D)=\frac{1}{28}\)です。よって、情報Dの情報量は、
$$i(D)=-\log_2 P(D)=-\log_2 \frac{1}{28}=2+\log_2 7$$
となります。ここで、
$$i(D)=i(B\cap C)$$
となっていることに注目してください。情報Dというのは情報Bを得た後に情報Cを得るのと全く同じものです。よって、情報量は情報を得る経路によらないことが分かります。
平均情報量
最後に、平均情報量というものを考えます。平均情報量とは、その情報がもたらされたときに得られる情報量の期待値として定義されます。また具体例を通して考えます。
今度は、内通者が以下の2つの情報のいずれかを与えるものとしましょう。
\(I_1\):犯行は2月の第1週に決行される
\(I_2\):犯行は2月の第2週~第4週に決行される
①何も情報を持っていない場合
この場合、
$$P(I_1)=\frac{1}{4}, P(I_2)=\frac{3}{4}, i(I_1)=2, i(I_2)=-\log_2 \frac{3}{4}$$
だから、内通者がもたらす情報量の期待値、すなわち平均情報量は、
$$E_1=P(I_1)i(I_1)+P(I_2)i(I_2)=\frac{1}{2}-\frac{3}{4}\log_2 \frac{3}{4}$$
となります。
②情報Aを得ている場合
情報A(「2月の前半に決行される」)を既に得ている場合、
$$P(I_1)=\frac{1}{2}, P(I_2)=\frac{1}{2}, i(I_1)=1, i(I_2)=1$$
だから、内通者がもたらす情報量の期待値、すなわち平均情報量は、
$$E_1=P(I_1)i(I_1)+P(I_2)i(I_2)=1$$
となります。
以上から、平均情報量について次の公式が成り立つことが分かります。
公式
情報\(I_1, I_2, \dots , I_n\)のいずれかがもたらされるとき、平均情報量 \(E\)は、
$$E=\sum_{k=1}^n P(I_k)i(I_k)$$
である。ただし、\(P(I_k)\)は \(I_k\)が示す物事が起こる確率、\(i(I_k)\)は \(I_k\)の情報量で、\(i(I_k)=-\log_2 P(I_k)\)である。
情報量は何に役立つのか
ここまで、情報量の定義から平均情報量までひとつひとつ解説してきましたが、これが何の役に立つかというと、1つは「情報源符号化定理」を扱えるようになるということです。
これは情報の符号化についての限界を平均情報量を用いて表すものであり、次回解説します。
3行まとめ
このページでは情報量の性質や求め方、平均情報量について解説しました。まとめると以下の通りです。
- 情報量とはある情報にどのぐらい情報が含まれているかを示す指標である。
- 情報量 \(i(X)\)は \(X\)が起こる確率 \(P(X)\)を用いて \(i(X)=-\log_2 P(X)\)で定義される。
- ある情報がもたらす情報量の期待値を平均情報量という。
皆様の参考になれば幸いです。
当サイトでは教養としての情報科学を体系的に紹介しています。以下から当サイトの記事一覧をご覧いただけます。


