【検証】東大数学2025をChatGPTに解答させて採点してみた

昨今のAI、特に大規模言語モデルに基づいた対話型AIの進化には目を見張るものがあります。そこで今回は、高性能AIをもってすれば東京大学の入試にも太刀打ちできるのか、実際に問題を解かせて採点することで検証します。

筆者は昨年まで数年間にわたり、塾講師として大学受験生に数学を指導していました。東大理系数学の過去問指導も多数経験し、業務の一環として採点・添削も行っていました。そんな経験を活かし、実際にChatGPTの解答に点数をつけてみたいと思います。

Tamura

この記事を書いた人：

• 元塾講師アルバイト、現役東大生
• 東大理系数学の過去問指導も多数経験

検証の条件

今回の検証は以下の条件で実施します。

問題をTeX形式で与えるのは、今回は画像読み取りの性能を見たいのではなく、純粋に論理的な解答ができるかどうかを見たかったからです。

採点に用いる解答はこちら、難易度はこちらで、いずれも河合塾のものを参考にさせていただきます。

では早速、第一問から見ていきましょう。

第一問

問題

座標平面上の点 \( A(0,0) \), \( B(0,1) \), \( C(1,1) \), \( D(1,0) \) を考える。実数 \( 0 < t < 1 \) に対して, 線分 \( AB, BC, CD \) を \( t : (1-t) \) に内分する点をそれぞれ \( P_t, Q_t, R_t \) とし, 線分 \( P_tQ_t, Q_tR_t \) を \( t : (1-t) \) に内分する点をそれぞれ \( S_t, T_t \) とする。さらに, 線分 \( S_tT_t \) を \( t : (1-t) \) に内分する点を \( U_t \) とする。また, 点 \( A \) を \( U_0 \), 点 \( D \) を \( U_1 \) とする。
（1）点 \( U_t \) の座標を求めよ。
（2）\( t \) が \( 0 \leq t \leq 1 \) の範囲を動くときに点 \( U_t \) が描く曲線と, 線分 \( AD \) で囲まれた部分の面積を求めよ。
（3）\( a \) を \( 0 < a < 1 \) を満たす実数とする。\( t \) が \( 0 \leq t \leq a \) の範囲を動くときに点 \( U_t \) が描く曲線の長さを, \( a \) の多項式の形で求めよ。

東京大学2025年度前期試験 理系数学 より

＜難易度：標準（河合塾による）＞

ChatGPTの解答

採点

全体的にはよくできています。ですます調が気になりますが、問題ではありません。
（1）は満点です。最後の但し書きもよく書けています。Aや\( S_t \)は点なので数式の書き方に違和感がありますが、減点はされないでしょう。記述は多すぎで、解答用紙に収まらないでしょうが、今回は不問とします。
（2）は2点減点としました。解法の流れは良く計算も合っていますが、媒介変数表示された関数の積分を行う際はグラフが折り返さないか確認しなければなりません。ここは受験生がよく見落としがちな部分と言えます。なお、河合塾の解答で\( x'(t) \)が非負であることを明記しているのはこのためです。グラフが折り返している場合は、単純にt=0から1まで積分すればいいかは自明ではありません。また、\( y(t) \)が非負であることにも言及するのが望ましいです。
（3）は満点です。立式も、計算過程の絶対値の外し方も大変良いです。結果もあっています。

第二問

問題

（1）\( x > 0 \) のとき, 不等式 \( \log x \leq x – 1 \) を示せ。
（2）次の極限を求めよ。
\[ \lim_{n \to \infty} n \int_{1}^{2} \log \left( \frac{1 + x^{\frac{1}{n}}}{2} \right) dx \]

東京大学2025年度前期試験 理系数学 より

＜難易度：やや難（河合塾による）＞

ChatGPTの解答

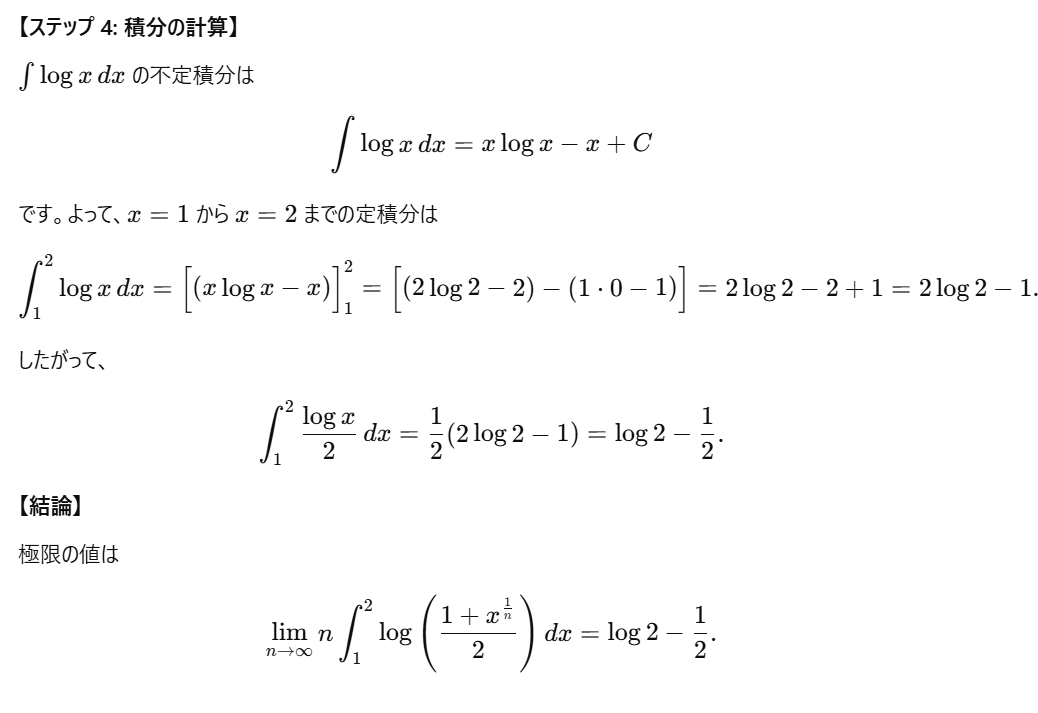
採点

（1）は満点です。増減表を書いて端的に記述して欲しいところではあります。
（2）は高校範囲を超えた解答となりました。（1）の意味を考え、はさみうちの原理に持ち込んで欲しかったところです。東大は大学数学を用いても論理に穴が無ければ減点されないとよく言われます。しかし今回は、ステップ2の式変形に飛躍があること、ステップ3で積分と極限を断りなく入れ替えていることにより、大きな減点は免れないでしょう。結果は合っているので5点としました。

第三問

問題

平行四辺形 \( ABCD \) において, \( \angle ABC = \frac{\pi}{6} \), \( AB = a \), \( BC = b \), \( a \leq b \) とする。次の条件を満たす長方形 \( EFGH \) を考え, その面積を \( S \) とする。
　条件：点 \( A, B, C, D \) はそれぞれ辺 \( EF, FG, GH, HE \) 上にある。
ただし, 辺はその両端の点も含むものとする。
（1）\( \angle BCG = \theta \) とするとき, \( S \) を \( a, b, \theta \) を用いて表せ。
（2）\( S \) のとりうる値の最大値を \( a, b \) を用いて表せ。

東京大学2025年度前期試験 理系数学 より

＜難易度：標準（河合塾による）＞

ChatGPTの解答

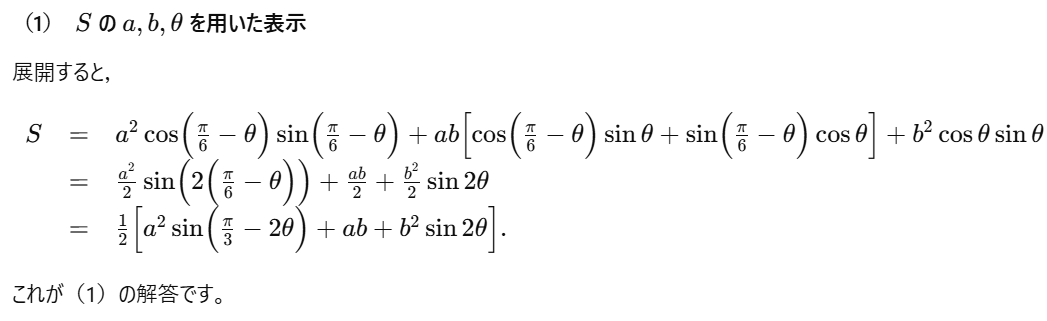
採点

まず全体をxy座標系に配置したようです。受験数学ではよく「最後の手段」と言われますが、解答を見るとテクニカルな計算を繰り返し巧みに処理しきりました。こういった問題を解く際は、まず図を書けというのが鉄則ですが、図形的な性質を全く使っていない（使えない）のがいかにも言語モデルといった感じです。（図を書かずにこれはかなりすごいとも言える。）難易度が上がったせいか、意味不明な文字が紛れていますが、目をつむりましょう。
（1）は満点です。（1）に入る前の考察で適切に解答を導けています。
（2）は8点減点としました。\( S(\theta) \) の式だけを見て処理すると上の解答のようになりますが、これは正解とは言えません。なぜなら、最大値をとる\( \theta \) が実際に存在するかが不明であるからです。\( \theta \) は図形的な制約を受けるため、a, bが（\( a\leq b \) なる）どのような値であっても、最大値をとれるかは分からないのです。実際、今回はa, bの条件次第で最大値が変わってきます。場合分けの議論ができていないこと、場合分け2通りのうち1通りの答えを出せていることから、12点中の4点としました。

ちなみに、かなり長い解答となっていますが第三問は解答用紙が大きいので問題はないでしょう。

第四問

問題

この問いでは, 0 以上の整数の 2 乗になる数を平方数と呼ぶ。\( a \) を正の整数とし, \( f_a(x) = x^2 + x – a \) とおく。
（1） \( n \) を正の整数とする。\( f_a(n) \) が平方数ならば, \( n \leq a \) であることを示せ。
（2）\( f_a(n) \) が平方数となる正の整数 \( n \) の個数を \( N_a \) とおく。次の条件 (i), (ii) が同値であることを示せ。
(i) \( N_a = 1 \) である。
(ii) \( 4a + 1 \) は素数である。

東京大学2025年度前期試験 理系数学 より

＜難易度：標準（河合塾による）＞

ChatGPTの解答

採点

（1）は満点です。背理法を使った過不足ない証明になっています。
（2）も満点です。第三問（1）と同様に文字の置き方、式変形の仕方が非常にテクニカルで驚かされます。論理にも穴はないようです。最後の同値性の確認において若干記述が重複している点はありますが、全体としては、解答まで一直線に進む非常に優れた構成になっています。

第五問

問題

\( n \) を 2 以上の整数とする。1 から \( n \) までの数字が書かれた札が各 1 枚ずつ合計 \( n \) 枚あり, 横一列におかれている。1 以上 \( (n-1) \) 以下の整数 \( i \) に対して, 次の操作 \( (T_i) \) を考える。

\( (T_i) \) 左から \( i \) 番目の札の数字が, 左から \( (i+1) \) 番目の札の数字よりも大きければ, これら 2 枚の札の位置を入れかえる。そうでなければ, 札の位置をかえない。

最初の状態において札の数字は左から \( A_1, A_2, \dots, A_n \) であったとする。この状態から \( (n-1) \) 回の操作 \( (T_1), (T_2), \dots, (T_{n-1}) \) を順に行った後, 続けて \( (n-1) \) 回の操作 \( (T_{n-1}), \dots, (T_2), (T_1) \) を順に行ったところ, 札の数字は左から \( 1, 2, \dots, n \) と小さい順に並んだ。以下の問いに答えよ。

（1）\( A_1 \) と \( A_2 \) のうち少なくとも一方は 2 以下であることを示せ。
（2）最初の状態としてありうる札の数字の並び方 \( A_1, A_2, \dots, A_n \) の総数を \( c_n \) とする。\( n \) が 4 以上の整数であるとき, \( c_n \) を \( c_{n-1} \) と \( c_{n-2} \) を用いて表せ。

東京大学2025年度前期試験 理系数学 より

＜難易度：やや難（河合塾による）＞

ChatGPTの解答

採点

（1）は無得点です。上の解答は背理法にも見えますが、証明すべき命題の対偶について論じているとすると分かりやすいと思います。（1）で証明すべき命題の対偶は、「\( A_1 \geq 3 \) かつ \( A_2 \geq 3 \) ならば、操作の結果、札の数字が左から \( 1, 2, \dots, n \) と小さい順に並ぶことはない」です。解答ではこれを「カード1が最も左に移動できない」ことだけで証明しようとしていますが、それを示す論理が不十分です。実際、例えば \( A_1 = 3, A_2=4, A_3 = 1 \) ならば操作の結果、カード1は最も左になります。「カード1が最も左に移動できない」は偽であり、カード2も考慮に入れる必要があります。
（2）も無得点です。場合①は、\( A_2 \geq 3 \) の場合を数えられていません。場合②も全く的外れです。無論、結果も正しくありません。

第六問

問題

複素数平面上の点 \( \frac{1}{2} \) を中心とする半径 \( \frac{1}{2} \) の円の周から原点を除いた曲線を \( C \) とする。
（1）曲線 \( C \) 上の複素数 \( z \) に対し, \( \frac{1}{z} \) の実部は 1 であることを示せ。
（2）\( \alpha, \beta \) を曲線 \( C \) 上の相異なる複素数とするとき, \( \frac{1}{\alpha^2} + \frac{1}{\beta^2} \) がとりうる範囲を複素数平面上に図示せよ。
（3）\( \gamma \) を (2) で求めた範囲に属さない複素数とするとき, \( \frac{1}{\gamma} \) の実部がとりうる値の最大値と最小値を求めよ。

東京大学2025年度前期試験 理系数学 より

＜難易度：標準（河合塾による）＞

ChatGPTの解答

採点

（1）は満点です。巧みな式変形で正解にたどり着きました。
（2）は1点減点としました。存在範囲を示す問題という特性上、解答中盤の「任意の固定 \(p\) に対して最大値は \( t_1 t_2 = \frac{p^2}{4} \) 」についてより詳細な説明が必要だと考えました。なお、この問題は「図示せよ」となっていますが、今回は範囲を正しく記述するまでで正解とします。
（3）は1点としました。結果は合っていますが、解答中盤の「極値は、境界 \( u=2-\frac{v^2}{8} \) で達成されると考え」が致命的にまずいです。今回は結果的に境界上で最大・最小値がとられていますが、いわゆる「予選・決勝法」などを用いて2変数関数の最大・最小問題として丁寧に考察を積み上げる必要があります。境界線上以外の領域について考察できていない以上、点数は入りません。ただ、考察の対象となる式 \( \frac{u}{u^2+v^2} \) を導いている点で初期の方向性は正しいため、1点加点しました。

最終結果

合計得点は120点中70点（得点率58.3％）となりました。数学においては、十分に合格ラインに達していると言えます。

全6問の解答を振り返ると、「式変形が非常に得意」という印象でした。第三問（1）は非常に多くの文字を使って正解にたどり着いていましたし、第四問も論理的思考と組み合わせて適切に論証してみせました。

一方で、図やグラフを描いて状況を整理していく問題については弱点となったようです。言語モデルなので当然ではあるのですが、グラフも増減表も一切描かずに解答していました。そのため第三問（1）はかなり遠回りしていましたし、（2）は図形的な制約を見逃しました。第五問も状況を整理しきれませんでした。

現状のChatGPTによる解答は、「参考書の解答を読みまくって独学で勉強してきた受験生」のような印象を受けます。圧倒的な計算・式変形テクニックで押し切っている感じです。筆者の経験上、そのような受験生は「図を描いて状況を整理する」ことを覚えると一気に成績が伸びます。これはChatGPTも同じでしょう。すなわち、入力を受け取る段階だけでなく、推論の段階でも自ら図を生成し活用する「マルチモーダル推論モデル」なるものが登場すれば、また一歩、大きく能力が向上しそうです。さらに言えば、これは数学の問題を解くことに限った話ではないでしょう。

発展の余地があると言いつつも、現状の解答は十分に驚異的であり、AIの進化を見せつけられました。大学受験レベルの数学の指導がAIに置き換わるのはそう遠くはないのかもしれません。