論理演算とは、真(True,1)と偽(False,0)の2つの値を用いて行う演算のことで、コンピューターの2進数による演算は論理演算の膨大な積み重ねで実現されています。具体的には、「AND」や「OR」などの様々な論理回路によって実行されますが、このページではその一覧を示し、ブール代数についても触れていきます。
このページでは、
- 論理回路の一覧【図解】
- 完備性について
- ブール代数とは
を解説しています。
論理回路とは
論理回路(論理関数)は、0や1を入力するとそれぞれの回路に応じて0や1を出力するものです。電子回路の中で非常に多く使われています。例えば、電子レンジは「スイッチを押す」かつ「扉が閉まっている」状態でないと動きませんが、これには「かつ」を示すAND回路が使われます。
以下で代表的な7種類を解説します。また、それぞれの論理回路について図に描く際の標準の描き方(MIL記法)が定められているので、併せて示します。
以下のベン図ではAやBの丸の中がAやBの値が1であることを示し、赤い部分で1を出力することを表すこととします。また、論理回路の入力と出力をまとめた表を真理値表といい、これも併せて示します。(ベン図と真理値表は本質的に同様の表現で、どちらかを理解すれば十分です。)
NOT
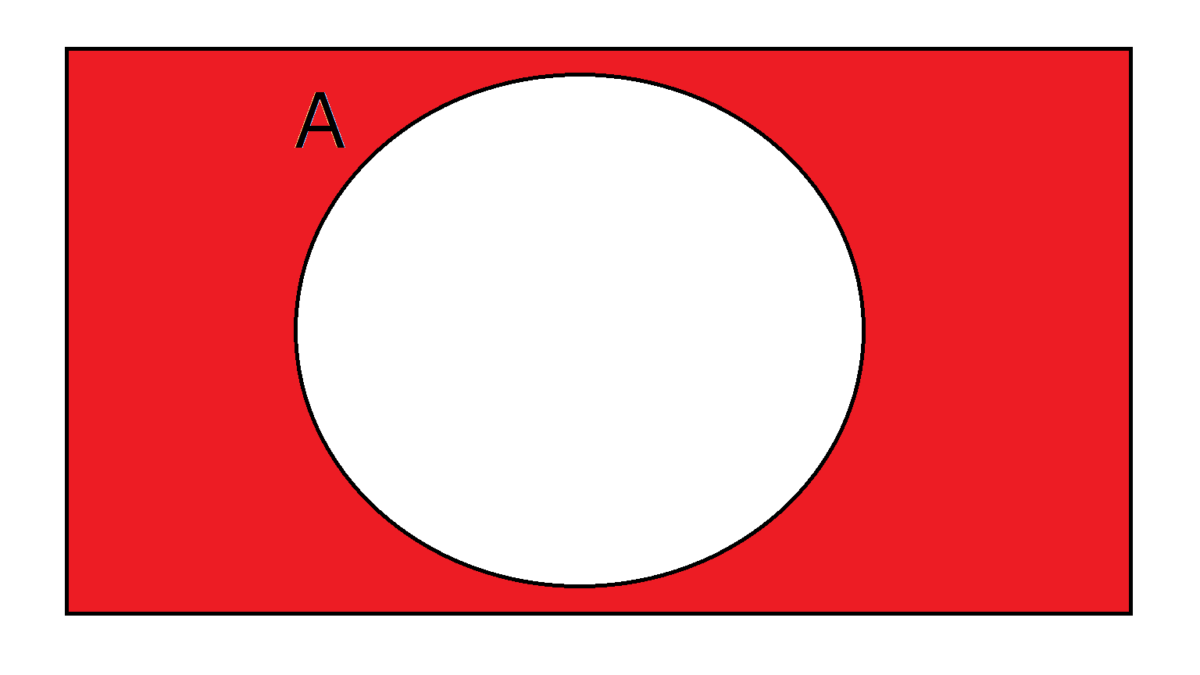
NOT(A)は、入力値と逆の値を出力します。
真理値表:
| A | 出力 |
| 1 | 0 |
| 0 | 1 |
MIL記法:
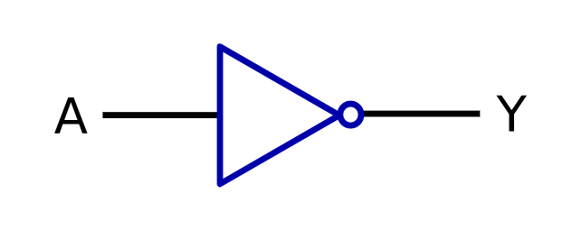
AND
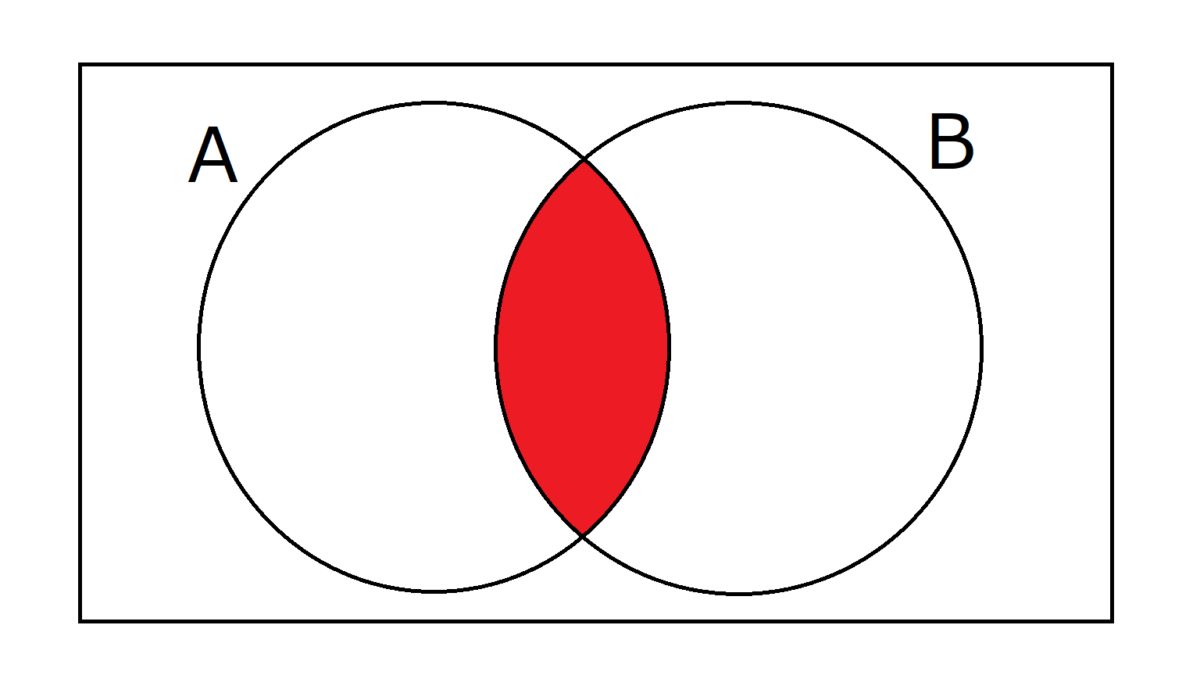
AND(A,B)は、両方1のときのみ1を出力します。「かつ」であり、論理積とも呼ばれます。
真理値表:
| A | B | 出力 |
| 1 | 1 | 1 |
| 1 | 0 | 0 |
| 0 | 1 | 0 |
| 0 | 0 | 0 |
MIL記法:
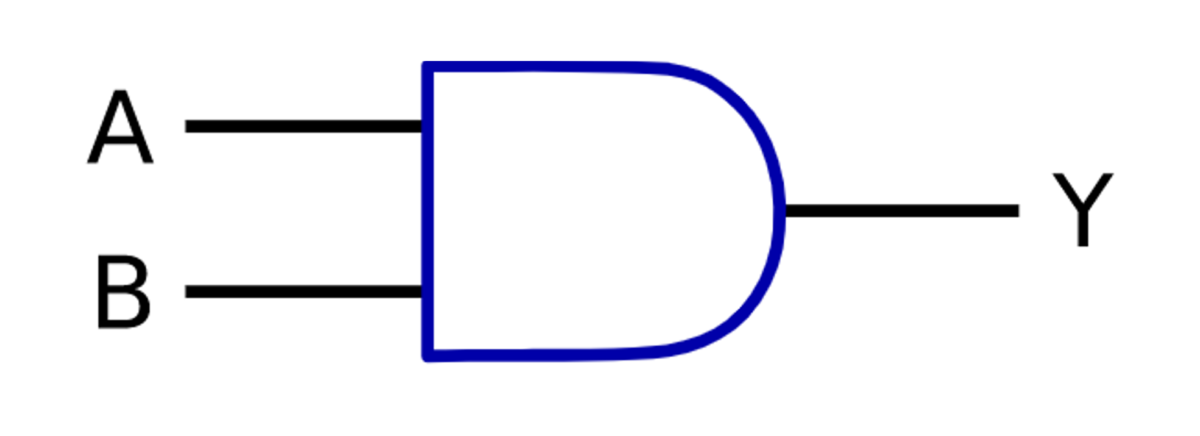
OR
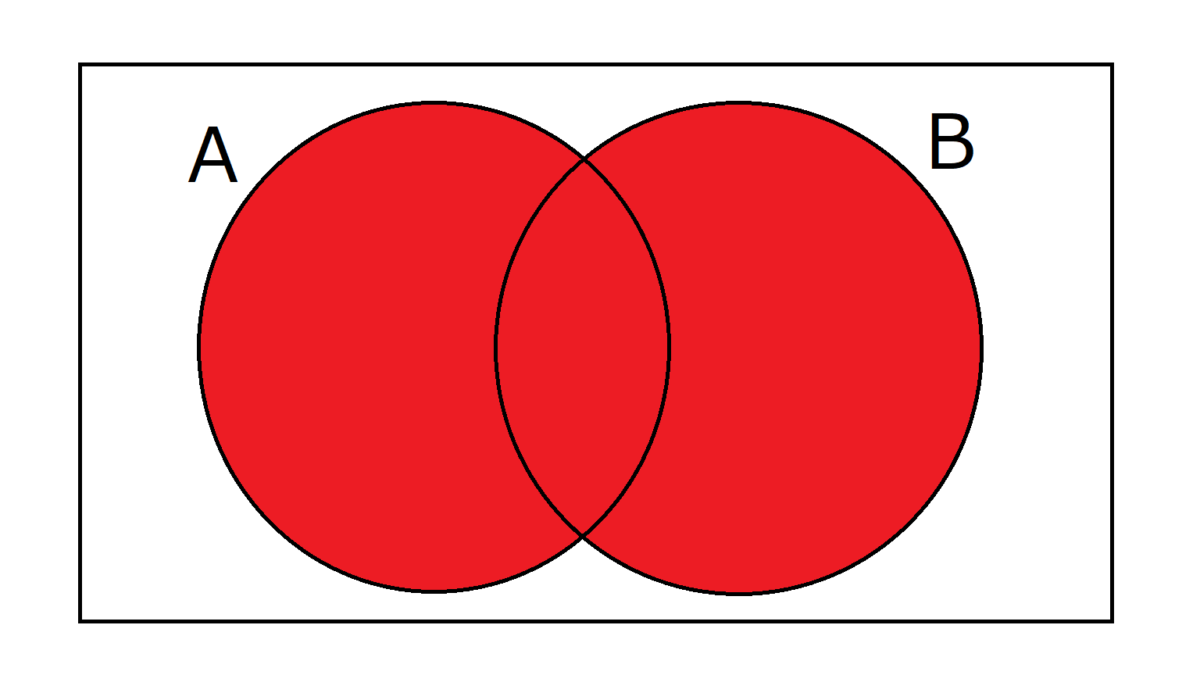
OR(A,B)は、少なくとも一方が1のとき1を出力します。「または」であり、論理和とも呼ばれます。
真理値表:
| A | B | 出力 |
| 1 | 1 | 1 |
| 1 | 0 | 1 |
| 0 | 1 | 1 |
| 0 | 0 | 0 |
MIL記法:
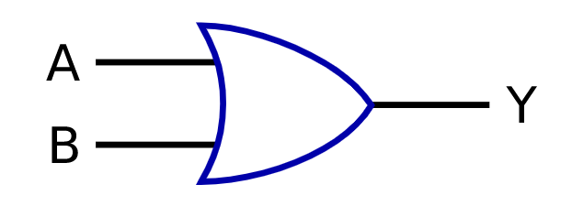
NAND
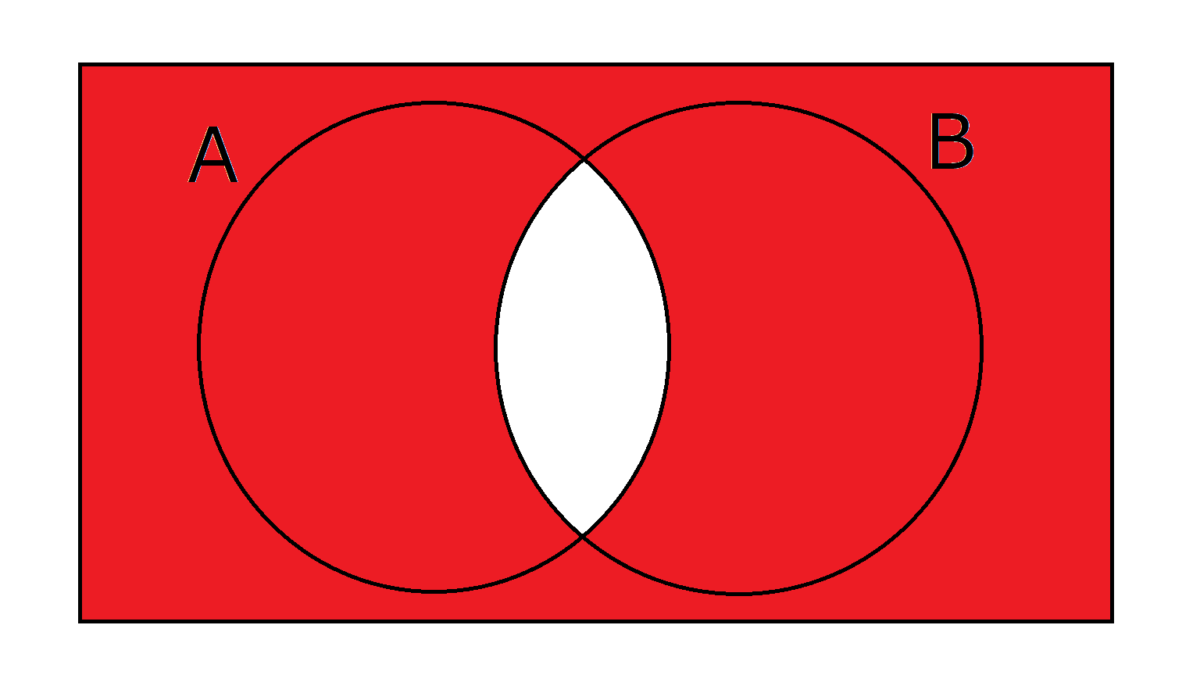
NAND(A,B)は、ANDの否定でありNOT(AND(A,B))とも表記できます。
真理値表:
| A | B | 出力 |
| 1 | 1 | 0 |
| 1 | 0 | 1 |
| 0 | 1 | 1 |
| 0 | 0 | 1 |
MIL記法:
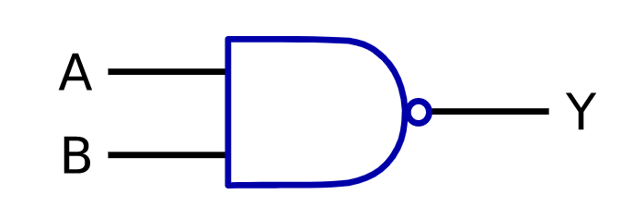
NOR
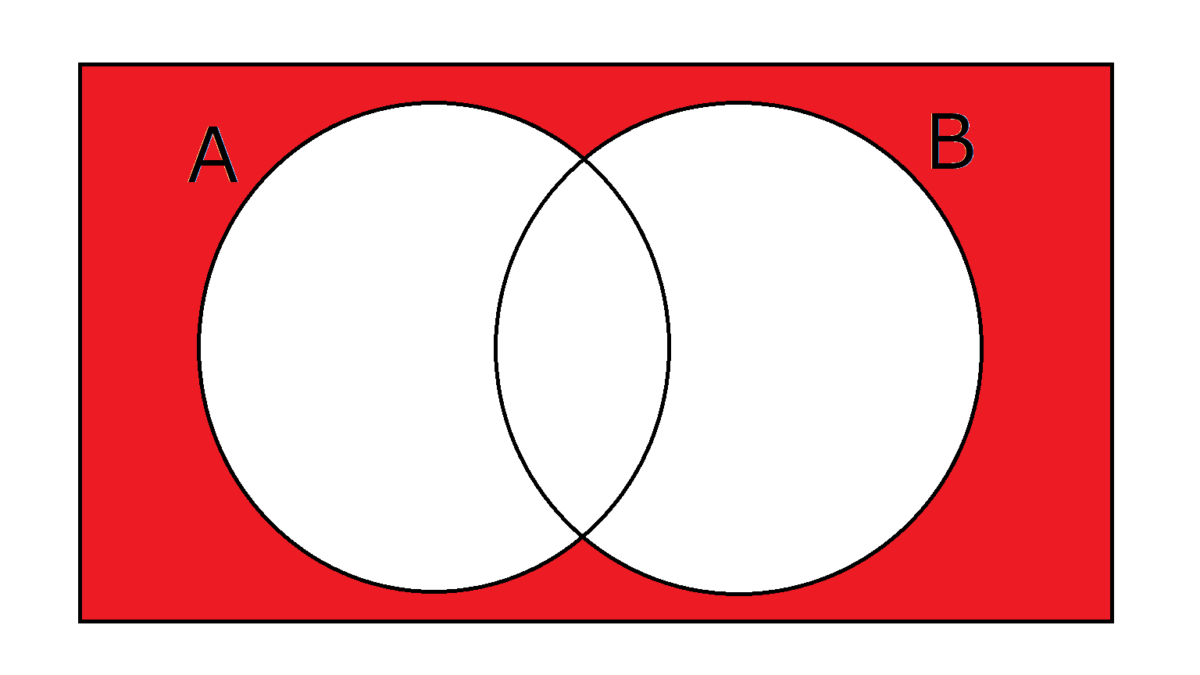
NOR(A,B)は、ORの否定でありNOT(OR(A,B))とも表記できます。
真理値表:
| A | B | 出力 |
| 1 | 1 | 0 |
| 1 | 0 | 0 |
| 0 | 1 | 0 |
| 0 | 0 | 1 |
MIL記法:
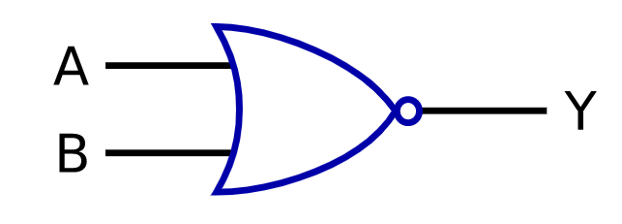
XOR
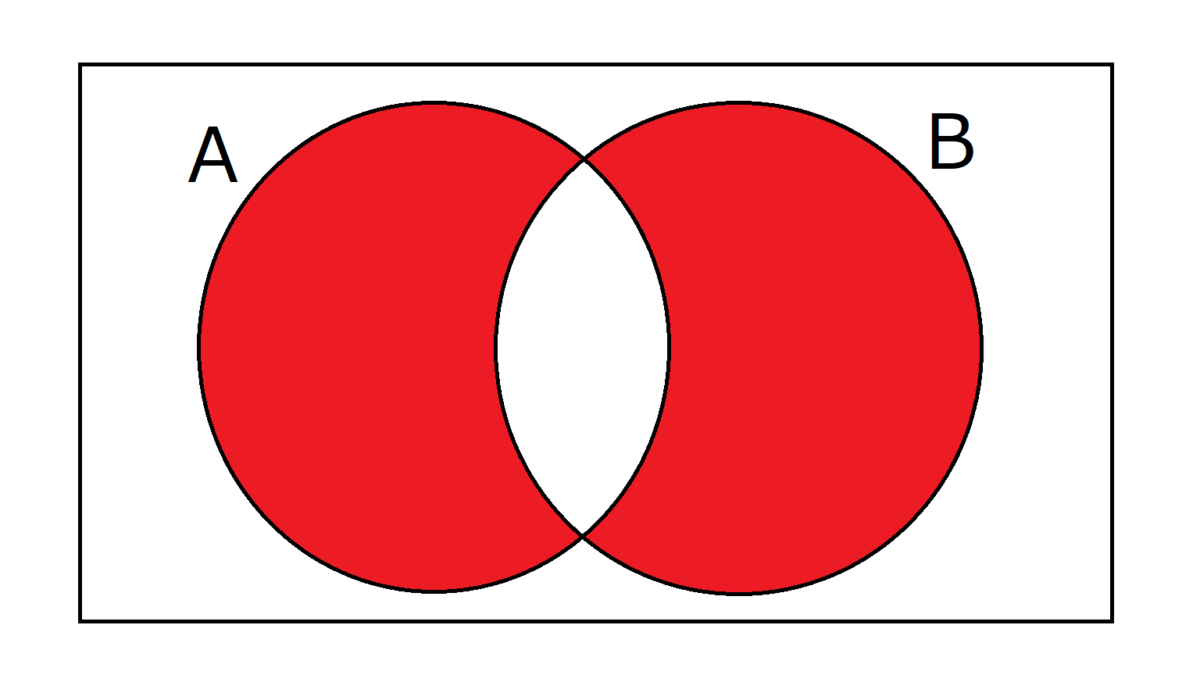
XOR(A,B)は、ORからANDを引いたものであり、排他的論理和(Exclusive OR)とも呼ばれます。
真理値表:
| A | B | 出力 |
| 1 | 1 | 0 |
| 1 | 0 | 1 |
| 0 | 1 | 1 |
| 0 | 0 | 0 |
MIL記法:
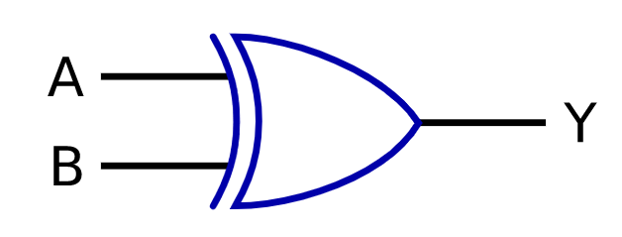
EQ(XNOR, NXOR)
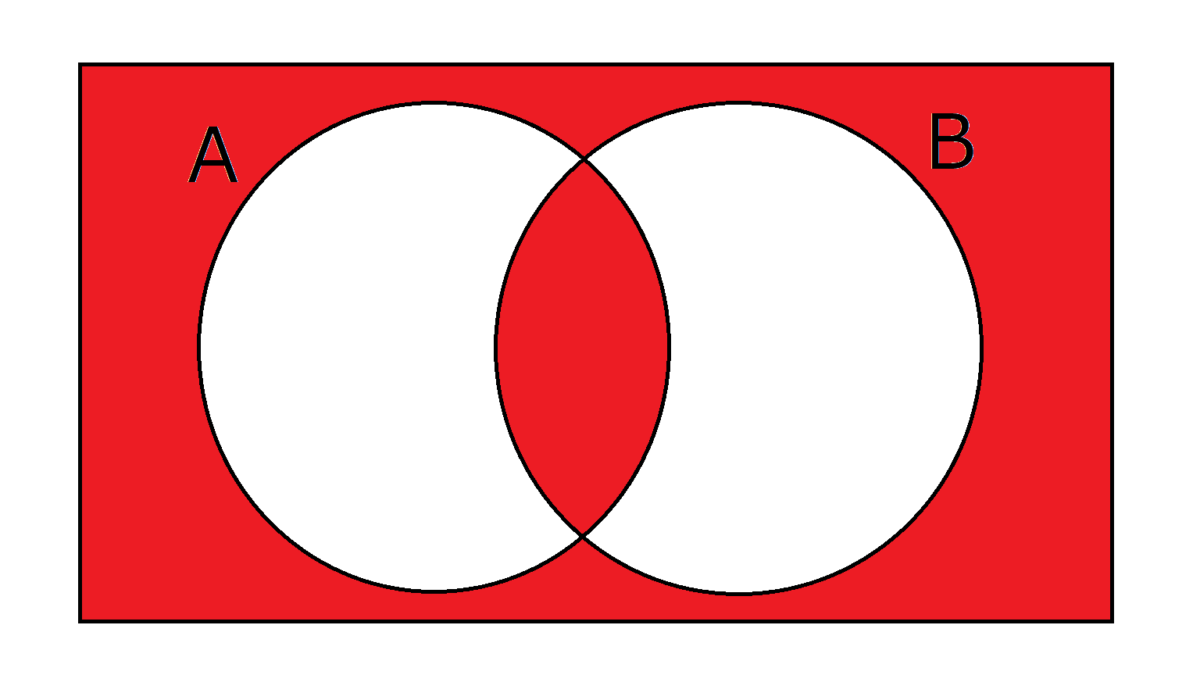
EQ(A,B)は、AとBの値が同じ時に1を出力します。EQはEquivalence(同値)の頭文字です。NOT(XOR(A,B))とも表記できます。
真理値表:
| A | B | 出力 |
| 1 | 1 | 1 |
| 1 | 0 | 0 |
| 0 | 1 | 0 |
| 0 | 0 | 1 |
MIL記法:
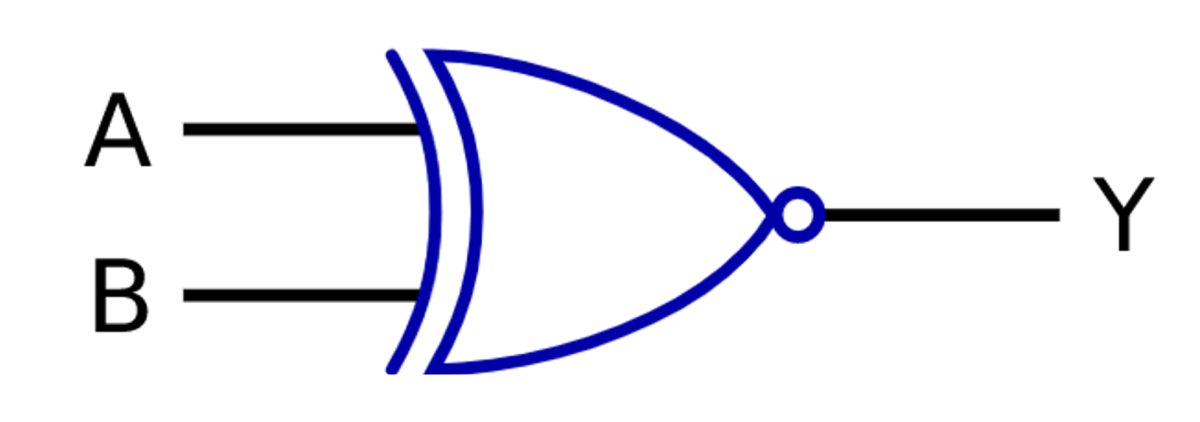
【発展】完備性について
以上で示した7つの論理回路は、以下のように、「NAND」または「NOR」だけで表現できることが知られています。このことから、「NAND」と「NOR」は汎用論理回路(Universal Logic Gates)と呼ばれることもあります。
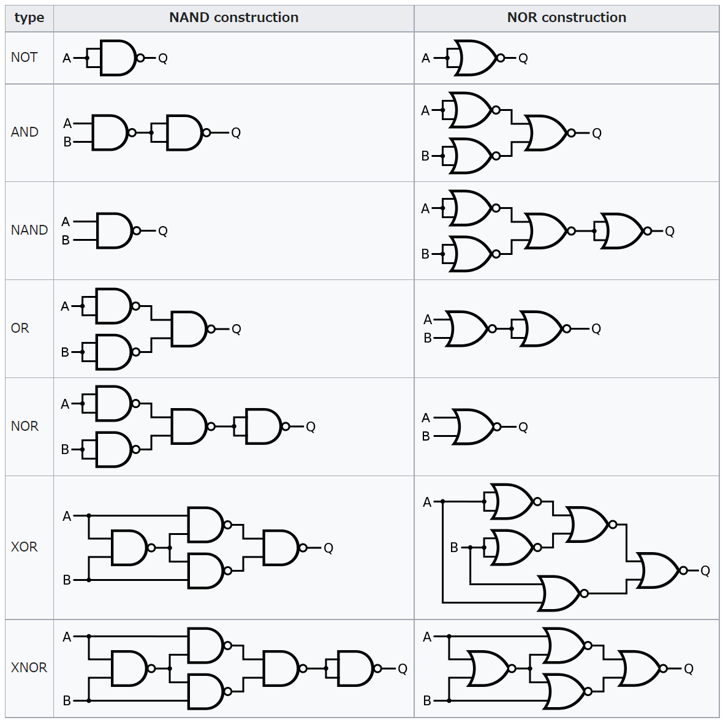
上記の{NAND}や{NOR}に加えて、{AND, NOT}(ANDとNOT)、{OR, NOT}(ORとNOT)でも全ての論理回路を表現できます。このような回路は、完備性(Functional Completeness)があると言われます。
ブール代数
真(True,1)と偽(False,0)の2つの値のみを用いて演算を行う数学を、ブール代数と呼びます。論理回路を数学的にとらえることは、様々な回路を設計するときに役に立ちます。
ブール代数における演算には、基本的に論理積、論理和、論理否定の3つがあります。
論理積
論理積はANDのことであり、「・」で表されます。上記のANDと全く同様に以下の式が成り立ちます。
0・0=0
0・1=0
1・0=0
1・1=1
論理和
論理和はORのことであり、「+」で表されます。上記のORと全く同様に以下の式が成り立ちます。
0+0=0
0+1=1
1+0=1
1+1=1
論理否定
論理否定はNOTのことであり、「\(\bar{x}\)」(バー)で表されます。上記のNOTと全く同様に以下の式が成り立ちます。
\(\bar{1}=0\)
\(\bar{0}=1\)
3行まとめ
このページでは論理回路やブール代数について解説しました。まとめると以下の通りです。
- 論理回路は、0や1を入力するとそれぞれの回路に応じて0や1を出力するもので、ANDやXORなど様々な種類がある。
- NANDやNORはそれだけで他の全ての論理回路を表せる(完備性)。
- ブール代数では、論理積(AND,「・」)、論理和(OR,「+」)を用いて論理演算を数学的に表現する。
皆様の参考になれば幸いです。
当サイトでは教養としての情報科学を体系的に紹介しています。以下から当サイトの記事一覧をご覧いただけます。


本ページでは、最も基本的な論理回路である「2入力1出力」のもの(とNOT)を紹介しています。