計算量とは、アルゴリズムの優秀さを計る指標の1つであり、プログラムの実行に必要な時間を、計算の回数という観点から示してくれるものです。これにより他のプログラムと比べて、処理に要する時間が相対的に長いのか短いのかを評価できます。本サイトで紹介する情報科学の中では情報量と並んでつまずきやすい分野ですが、丁寧に解説していきます。
このページでは、
- 計算量とは何か
- 実際の使い方
- 計算量のオーダーの求め方
を解説しています。
優秀なアルゴリズムとは
アルゴリズムの優秀さを判断したいというとき、その基準はなんでしょうか。バグがない、拡張性が高い…などなどいろいろあると思いますが、最も重要なものの1つは「短い時間で実行できる」でしょう。
例えばコンビニのレジに繋がっている商品管理システムが非常に貧弱で、商品を「ピッ」とするたび5秒待たされたとしたらたまったものではありません。
ただ、処理にかかる時間をそれぞれのアルゴリズムで計測し比べればいい、といった単純な話ではありません。
↓「アルゴリズム」が何か確認したい方はこちら
プログラムの実行にかかる時間を測るだけでは、以下のような問題点をうまく解決できません。
- 機器によって性能が違うこと
- 実際に使うときは扱うデータの大きさがバラバラであること
そこで、プログラム中の「計算回数」に着目した計算量という指標を用います。
計算量とオーダー記法
計算量は、扱うデータの大きさをnとして、プログラムの実行に必要な計算回数をnを用いて表したものです。例えば、以下のようなデータベースを用いて支払い金額を求めるプログラムを考えます。
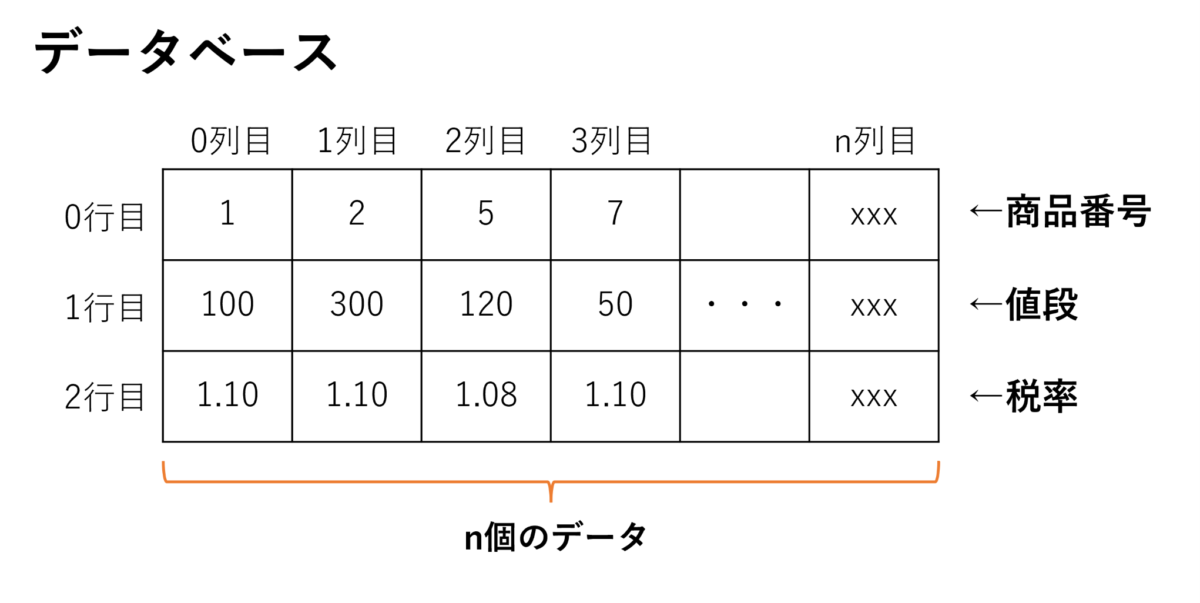
※商品番号は欠番がありますが小さい順に並んでいるとします。
計算量を具体的に求める
バーコードリーダーで読み取った商品番号をデータベースと照らし合わせて値段の情報を取得し、それに税率を掛けて表示することを考えます。では、商品番号をデータベースでどのように検索するのでしょうか。最初に思いつくのは次のような線形探索法でしょう。
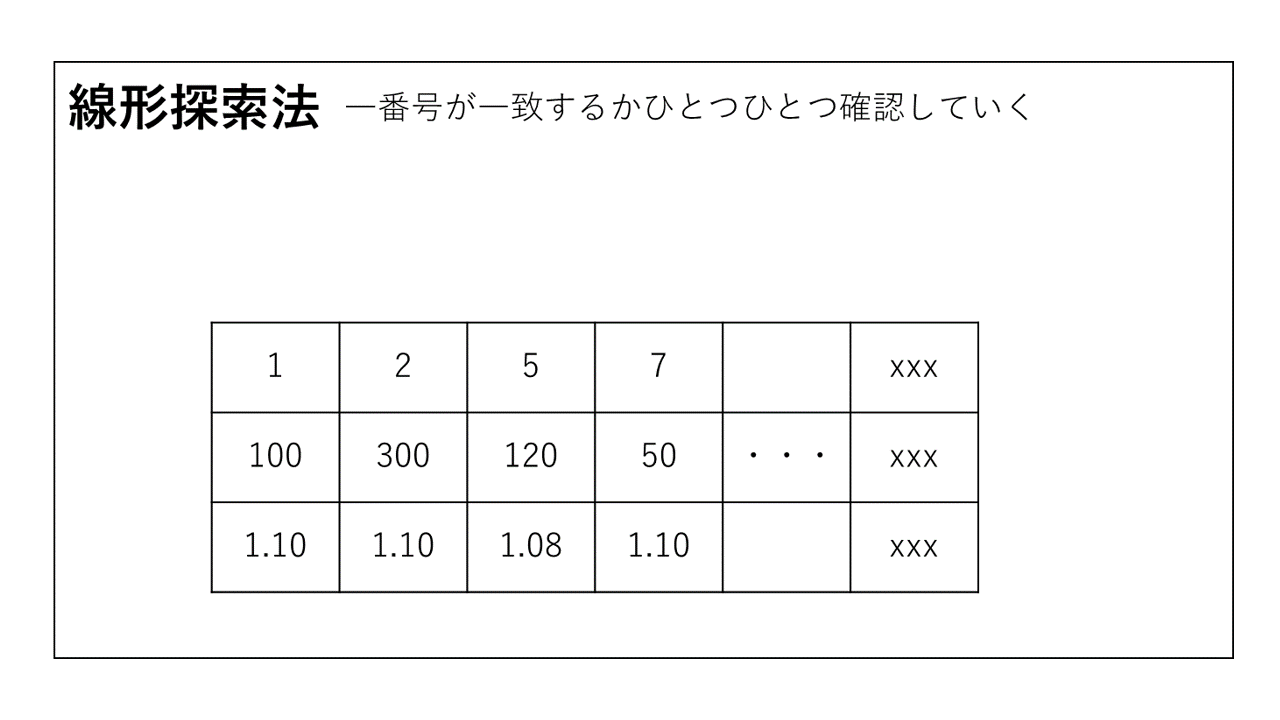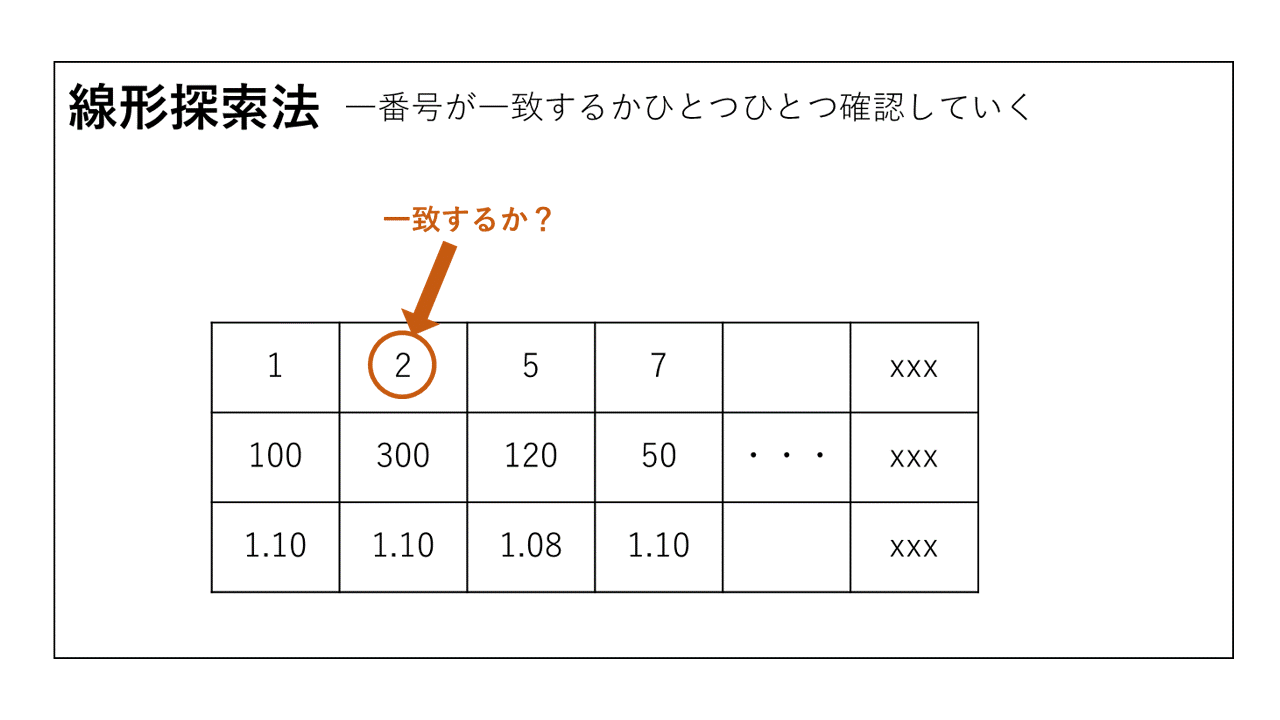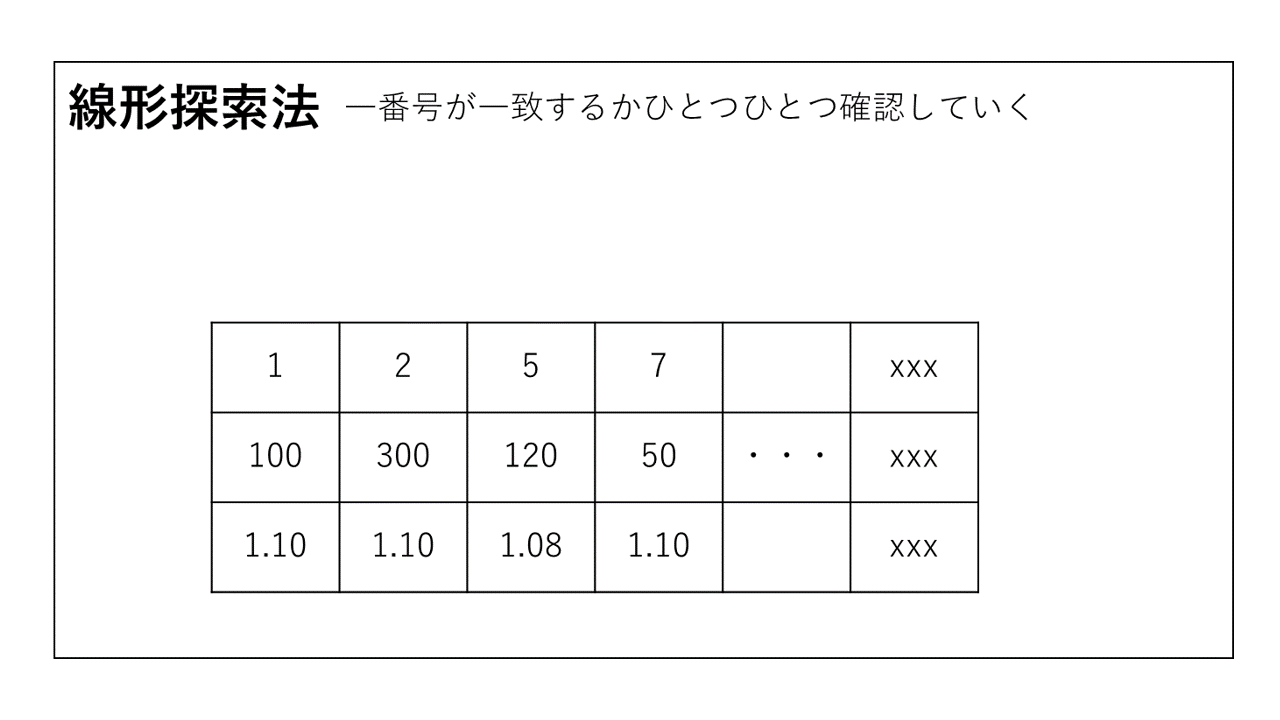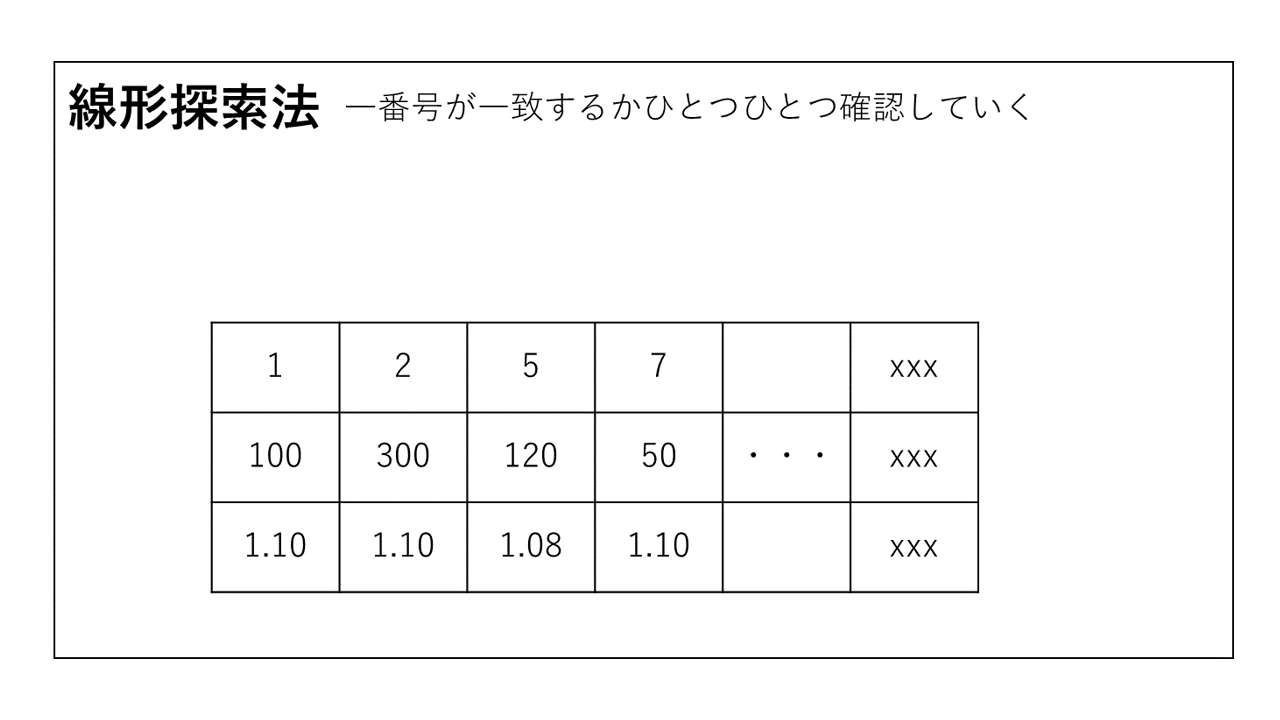
先頭のデータから末尾のデータまで商品番号が一致するものを探します。このアルゴリズムを用いたプログラムは次のようになります。
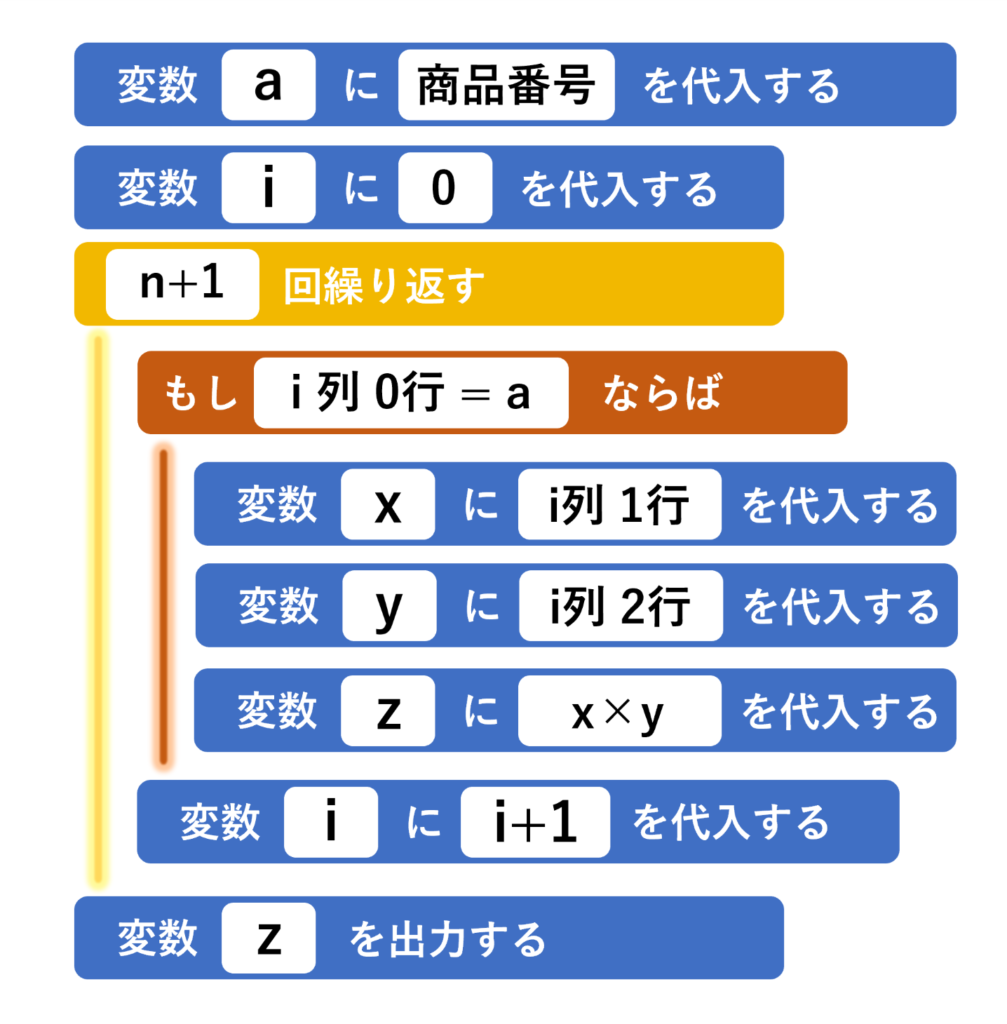
では、計算量を求めてみましょう。商品番号をデータベースで検索する際に、変数iに1を足す計算をn+1回、その後税込みの値段を求める計算を1回行っているので、計算量はn+2となります。
オーダー記法
先ほど実際に計算量を求めましたが、実際にプログラムを使う際には、nは数千とも数万ともなるのが普通であり、+2のような定数は無視しても何の不都合もありません。さらに言えば、nが大きいときアルゴリズムによって計算回数は何桁も変わってくるため、nの係数も無視してOKです。計算量がnの式で表されるのか、nの2乗の式で表されるのかだけが重要なのです。この考え方を表現するのがオーダー記法です。
オーダー記法
「その式がどんな関数で表されているのか」のみに着目する。以下のルールがある。
- 定数項は無視する。
- 定数倍は無視する。
- 増加のペースが小さい部分は無視する。
(例えば、\(n^2+2n\) の \(2n\) の部分は無視する。) - (nの式)\(=O(n^2)\) などと書く。
例:
- \(3n^2-2n+1=O(n^2)\)
- \(2n\log_a n=O(n\log n)\)
- \(3^n+2^n-5n^2=O(3^n)\)
- \(n^2+1000n=O(n^2)\)
このオーダー記法を用いると、先ほど求めた計算量は \(O(n)\) と表されます。このようにオーダー記法で表した計算量を、計算量のオーダーまたは漸近計算量と言います。「計算量を求める」とはふつう、この計算量のオーダーを求めることを指します。
参考:オーダー記法(ランダウの記法)の数学的理解
\(f(x)=O(g(x))\) であるとは、\(x\) が十分に大きいとき \(f(x)\) が \(g(x)\) かその定数倍で上から抑えられることを言います。これはつまり、以下が成り立つということです。
$$\lim_{x \to \infty} \frac{f(x)}{g(x)} が有限の値(0を含む)である$$
例えば、先述の通り \(3n^2-2n+1=O(n^2)\) ですが、ここで \(f(x)=3x^2-2x+1, g(x)=x^2\) とすれば、
$$\lim_{x \to \infty} \frac{f(x)}{g(x)}=\lim_{x \to \infty} \frac{3x^2-2x+1}{x^2}=3$$
であるためにこの式が成り立つわけです。この定義に従えば \(3x^2-2x+1=O(x^3)\) も正しいのですが、実用上意味のない式であるためふつうこのような表記はしません。
なお、\(f(x)=O(g(x))\) であることの数学的に厳密な定義は以下の通りです。
$$\exists x_0, \exists k > 0 \quad s.t. \quad \forall x: x > x_0 \Rightarrow |f(x)| < k|g(x)|$$
計算量と計算時間の目安
計算量の違いによって、実際にどのくらい計算時間が変わるのでしょうか。まず様々な関数について、1<n<100の範囲でグラフを描くと以下のようになります。
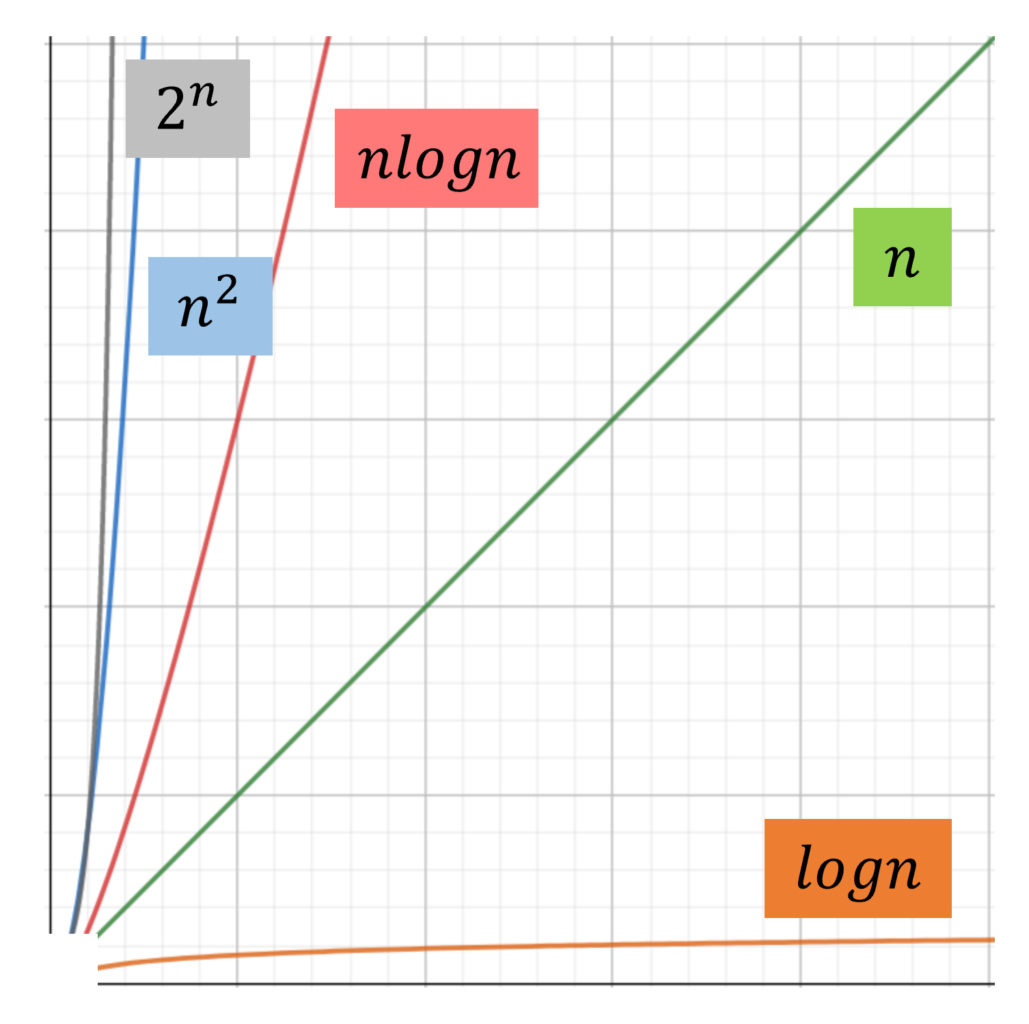
そして1秒間に \(10^8\) 回計算できるものとして、各計算量のアルゴリズムが計算に要する時間を求めた結果が以下の通りです。
| \(n\) の値→ ↓計算量 | \(10\) | \(10^2\) | \(10^4\) | \(10^8\) |
| \(\log n\) | 10ns | 20ns | 40ns | 80ns |
| \(n\) | 100ns | 1µs | 100µs | 1s |
| \(n\log n\) | 100ns | 2µs | 400µs | 8s |
| \(n^2\) | 1µs | 100µs | 1s | 3年 |
| \(2^n\) | 10µs | 30兆年 | ||
| \(n!\) | 30ms | 3e142年 |
これを見れば、アルゴリズムの工夫の重要性が分かると思います。またオーダー記法で定数項や定数倍を無視するのも納得できるでしょう。
ところで、アルゴリズムの重要性を説く、いわゆる「組み合わせ爆発おねえさん」が登場する動画を日本科学未来館が公開しています。息抜きに見てみると面白いでしょう。
練習問題
最後にいくつか、アルゴリズムの計算量を求める練習をしましょう。
問題
以下のプログラムについて計算量のオーダーをそれぞれ求めよ。
補足:「 \(10^{-n}\) の精度で」とは、実際の値とのずれが \(10^{-n}\) 以下になるような近似値を求めるということ。
↓解答↓
↓
↓
解答
- 計算回数は、合計を求める足し算の \(n-1\) 回と \(n\) で割る1回の計 \(n\) 回です。よって計算量のオーダーは \(O(n)\) となります。
- 計算回数は、全ての2数の積を求める \({}_n C_2\) 回とその和を求める \({}_n C_2 -1\) 回で、合計は \(2\cdot {}_n C_2 -1=n^2-n-1\) 回です。よって計算量のオーダーは \(O(n^2)\) となります。
- いきなり \(n\) で考えるのは少し分かりづらいので、まず \(n\) が2の場合でプログラムの中身を考えましょう。 \(10^{-2}\) は0.01なので、0, 0.01, 0.02, 0.03, … について2乗を計算していき、 \(\sqrt{3}\) に達したら計算を終了します。 \(\sqrt{3}\) は1.732…なので、今回は1.74で終わります。よって、計算回数は1.74÷0.01+1=175回です。
これにならえば、一般の \(n\) については , \(0, 10^{-n}, 2\cdot 10^{-n}, 3\cdot 10^{-n}\) … について2乗を計算していき、 \(\sqrt{3}\) に達したら計算を終了すると分かります。よって計算回数はおよそ \(\sqrt{3}/10^{-n}=\sqrt{3}\cdot 10^n\) 回です。したがって計算量のオーダーは \(O(10^n)\) となります。
\(\sqrt{3}\) は1.732…と無限に続く数なので端数が出ますが、そもそもオーダーを求めるのが目標なのでこのような考えで十分です。 - 最初は0~3だった区間が、1回ごとに幅が半分になり、幅が \(10^{-n}\) 未満になると終了するので、計算回数は \(3/2^k<10^{-n}\) を満たす最小の \(k\) となります。(下図参照)
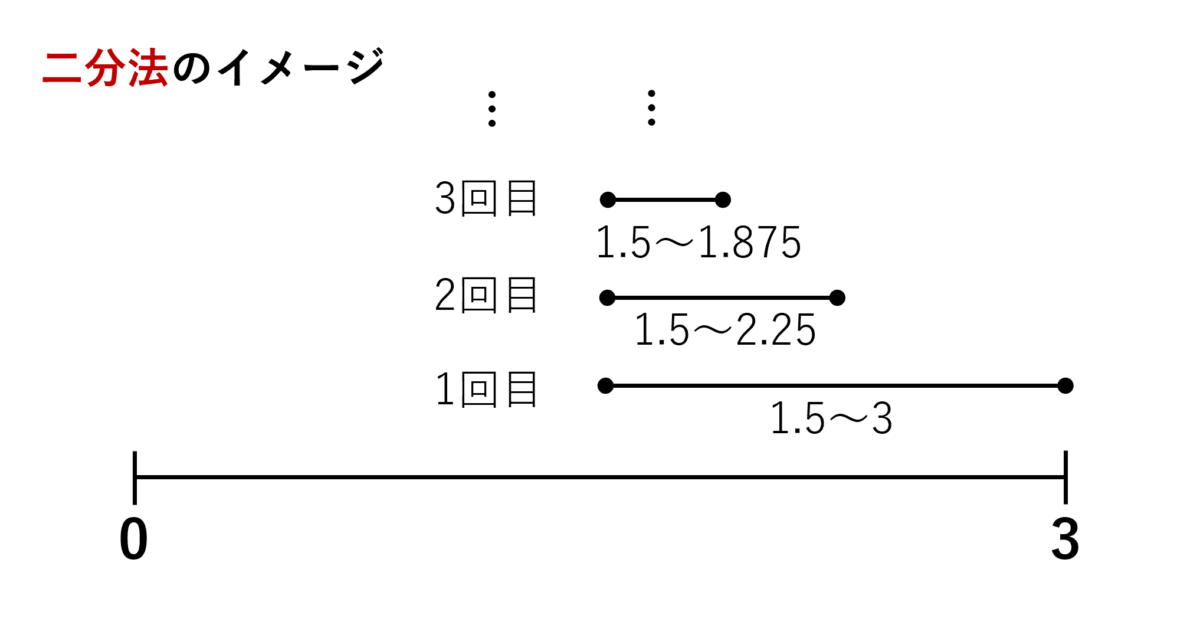
\(3/2^k=10^{-n}\) とすると \(k=\log_2 (3\cdot 10^n)=n\cdot \log_2 10 +\log_2 3\) なので、計算回数はおよそ \(n\cdot \log_2 10 +\log_2 3\) 回です。したがって計算量のオーダーは \(O(n)\)となります。
4.の別解
\(10^{-n}, 2\cdot 10^{-n}, 3\cdot 10^{-n}\) … 3の \(3\cdot 10^n\) 個の数値の中から二分探索を用いて最も \(\sqrt{3}\) に近い数値を求めると考えることができるので、計算回数は \(3\cdot 10^n/2^k\leq 1\) を満たす最小の \(k\) となります。\(3\cdot 10^n/2^k=1\) とすると \(k=n\cdot\log_2 10+\log_2 3\) なので、先ほどと同様に計算量のオーダーは \(O(n)\)となります。
4. の別解の中で導出されていますが、一般に、二分探索を用いて \(N\) 個のデータから1つのデータを見つけるときの計算量のオーダーは \(\log N\) となります。この性質を使うと素早く答えにたどり着けることも多くあります。
ニュートン法による平方根の計算については、計算量のオーダーは \(O(\log n)\) であるようです。
計算量のオーダーを求めるときは、まず計算回数の見当を付け、それをオーダー記法で表せばよい。
3行まとめ
このページでは、計算量について解説しました。まとめると以下の通りです。
- 計算量とは、扱うデータの大きさをnとしてプログラムの実行に必要な計算回数をnで表したもの。
- 実際には、計算量のオーダーで比較することが多い。
- 計算量のオーダーを求める際は、計算回数をだいたい見積もってからオーダー記法で表せばよい。
皆様の参考になれば幸いです。
当サイトでは教養としての情報科学を体系的に紹介しています。以下から当サイトの記事一覧をご覧いただけます。



上の例では、商品番号が一致した時点で検索を打ち切ることができます。この場合、計算量は状況によって変わりますが、計算量は最大でも(最悪でも)n+2であるということから、「最悪計算量はn+2である」と言います。実際の場面ではこのように計算量が一意に定まらないことが多いため、「最悪計算量」を単に「計算量」というのが普通になっており、本サイトでも以降は「最悪計算量」を指して「計算量」と記述することがあります。